El Laberinto se compone de un número indefinido de estancias semejantes. De todas ellas parten,
hacia otras estancias, un camino rojo y un camino azul; a todas ellas llegan, de otras estancias, un
camino rojo y un camino azul. Cada lugar es semejante a cada otro lugar y los caminos siempre
nos reconducen al punto de partida: repitiendo siete veces cualquier combinación de caminos
rojos y azules regresamos a donde estábamos. El enigma está en saber cuantas estancias
componen el Laberinto. ¿Puede haber un número infinito de ellas? ¿Puede haber un número
arbitrariamente grande?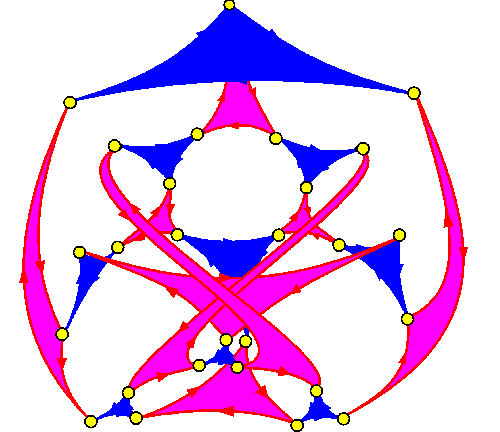
En 1897, William Burnside, profesor en el Royal Naval College de Greenwich, publica la primera edición de su tratado "La
teoría de los grupos". Burnside había publicado trabajos de investigación sobre teoría cinética de
los gases, teoría del oleaje (en conexión con la erupción del Krakatoa), el problema del potencial
y la teoría de las funciones automorfas, pero, en la actualidad, lo recordamos principalmente
como el creador, junto a Frobenius, de la teoría moderna de los grupos finitos.
Entre 1897 y 1902 Burnside plantea dos conjeturas extraordinariamente audaces, cuya
dilucidación dará pie a algunos de los leit motiv de la teoría de grupos durante el presente siglo.
Burnside conjetura que todo grupo simple no abeliano debe tener un número par de elementos.
65 años más tarde, Feit y Thompson, en uno de los trabajos más importantes del álgebra
moderna, demostrarían que esto es cierto. Burnside conjetura, o, más exactamente, se pregunta,
si un grupo con un número finito de generadores, en que cada elemento tiene orden finito, debe
necesariamente ser finito. La historia de esta segunda conjetura de Burnside, un caso particular de
la cual hemos escenificado utilizando un laberinto à la Borges, es harto compleja. Se trata,
además, de un tema de fuerte actualidad, por la concesión, en el Congreso Internacional de
Matemáticas, celebrado el pasado mes de agosto, de la medalla Fields a E.I. Zelmanov, por sus
trabajos sobre el llamado problema restingido de Burnside. |
En oposición al problema general,
aunque el PRB es, también, muy difícil, admite éste la utilización de algunas de las técnicas
desarrolladas por los algebristas a lo largo de este siglo. En particular, el PRB puede reformularse
fácilmente como un problema de álgebras de Lie: se trata de ver que las álgebras de Lie en
característica p que satisfacen ciertas condiciones, llamadas de Engel, son localmente nilpotentes.
La solución final afirmativa del PRB se presentó en el Congreso Internacional de 1990 y su autor
ha merecido la medalla Fields en el congreso de 1994. Se trata de Yefim Zelmanov, un
matemático de Novosibirks (residente actualmente en Estados Unidos) cuya vicisitud personal,
como la de tantos otros científicos de la antigua Unión Soviética, ha rayado el patetismo. Baste
mencionar, a título de ejemplo, que su carrera estuvo a punto de verse truncada cuando las
autoridades académicas, temerosas de enfrentarse a alguien que era claramente un genio, optaron
por suspenderle su tesis de doctorado, condenándole, de esta forma, a un ostracismo total en la
hermética sociedad soviética de la época. Es curioso observar que los resultados de Zelmanov sobre el PRB solo cubren el caso en que el orden es potencia de un número primo. El caso general requiere, además de los resultados de Zelmanov, del teorema de clasificación de los grupos simples, cuya validez es objeto de ciertas reservas por parte de la comunidad matemática (ver "La gran muralla China y el futuro del Algebra", La Vanguardia 13/6/92). Zelmanov se enfrentará ahora a la fama inherente a la medalla Fields y, al igual que Wiles cuando anunció la solución del problema de Fermat, se sentirá forzado a justificar, ante la opinión pública, la utilidad de su trabajo. Ni Proust ni Indurain han visto sometida su obra, bella, difícil e inútil, a la exigencia de la utilidad a corto plazo. Los matemáticos y los alpinistas, en cambio, se hallan cotidianamente enfrentados a la pregunta: ¿Para qué sirve este teorema? ¿Valía la pena subir allí arriba? Digamos, para empezar, que cualquier matemático reconoce immediatamente que la solución del PRB, obtenida por Zelmanov como la culminación del trabajo de muchos otros algebristas a lo largo de este siglo, es una pieza importante del conocimiento matemático, que se justifica a sí misma. ¿Es también una pieza útil? Desde luego, la hipotética utilidad práctica no ha jugado ningún papel en la motivación de Zelmanov (ni en la de Proust o Indurain). Pero, si los matemáticos abandonáramos uno sólo de nuestros campos de trabajo, por esotérico que pueda parecer visto desde el exterior, no cabe duda que los físicos, los biólogos, los economistas, los informáticos, tomarían el relevo, al cabo de muy poco tiempo, para desarrollar unas teorías sin las cuales sus investigaciones quedarían detenidas. La teoría de grafos, las álgebras de Lie de dimensión infinita, los cuerpos finitos, las formas cuadráticas, temas considerados hasta hace poco como paradigmas de la investigación "pura" forman parte, hoy, de los temas de investigación de los laboratorios más "aplicados" del mundo de la técnica. En un momento en que la matemática muestra, mejor que nunca, su extraordinaria aplicabilidad, los matemáticos reivindican poder seguir desarrollando su ciencia como han hecho siempre: por el mero placer de resolver cierto problema que un visionario sugirió, hace casi un siglo; por el mero placer de intentar comprender no sólo el gran laberinto del mundo, sinó los laberintos de todos los mundos posibles. Porque, tarde o temprano, veremos que aquellos laberintos también están aquí. |