La funció de suport, els convexes i els eriçons

Considerem per exemple la funció suport (sin(t))^3. Aleshores la parametrització és:

Fixat com es mou quan el paràmetre va de = a 2*Pi:

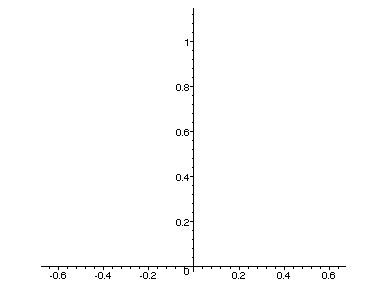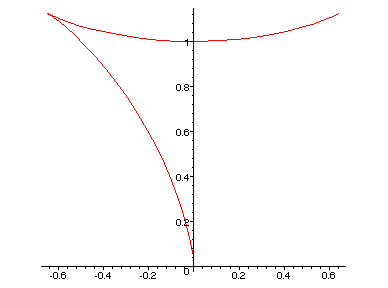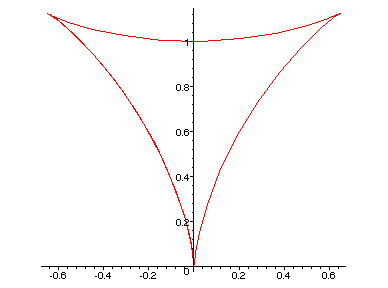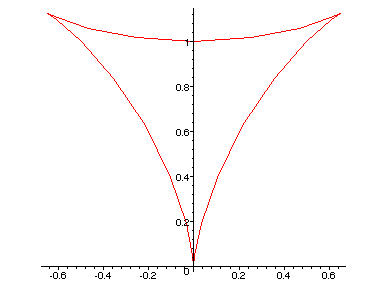
I la curvatura és sempre positiva

Algunes relexions de l'Agustí:

1. Orientacio positiva donada per la base canonica.
2. Curvatura amb signe=d angle/ds=(x'y''-y'y'')/(x'^2+y'^2)^3/2=k
3. dt/ds=kn on n es tal que t,n es positiva i t es la derivada i depen per tant de la parametrització.
4. Tot convex es suposa orientat contrerrellotge, aixi n apunta endins i per definicio de derivada com quocient incremental es clar que k positiva.
5. La curvatura d'un convex es positiva o zero.
6. Tot convex determina una funcio suport p, amb la definicio de Langevin i altres, com el suprem de les projeccions en cada direccio.
7. Si u pertany a S^1 i f(u) és el punt de la vora del convex amb tangent perpendicular a u que talla la recta generada per u en p(u)u (p la funcio suport) llavors u es normal exterior al convex.
8. L'aplicació de gauss es defineix girant la tangent 90 graus contrarellotge
9. La curvatura es MENYS el jacobia de l'aplicacio de Gauss
10. L'aplicació que defineix la vora del convex,f, és igual a MENYS l'aplicació de gauss.
11. La curvatura de la vora del convex, que sabem posiyiva o zero es igual a p+p'' i per tant p+p'' es positiu o zero.
12. q=-p dona lloc, al calcular l'envolupant, a un convex PERO no es funcio suport en el sentit langevin (Les figures son simetriques de manera que el suprem passa a ser l'infim !)
13. Si p es una funcio arbitraria deferenciable dues vegades de S^1 i fem l'envolupant en el sentit de santalo i p+p'' no s'anul.la mai tenim un convex. (Proof: si p+p'' es positiu es el de sempre. Si es negatiu posem q=-p i l'envolupant de q es convex i simetric del buscat que per tant es convex.

Uns eriçons