Hyperbolic circumference: center and radius

Given a point and a distance we can always construct a hyperbolic circumference with center in this point and radius the distance. In Workshop of Hyperbolic Geometry.pdf (in Catalan) we have seen the method to construct it. The steps we have followed to construct a hyperbolic circumference given the center and the radius are based in this method.

For using this tool we need to fix a system of coordinates. We need this system to give coordinates to the points and can use the formula that gives us the distance between two points. We want to use this formula since we have the radius of the circumference. The system will be fixed by the Sketchpad once the user will choose the tool.

To use this tool we will need to fix the boundary line, the center and the radius. First of all it is necessary to write the length of the radius with the option Measure/Calculate. Then, to mark the point and the measure of the radius that we have written. To create this tool we can follow these steps:

  1. Plot the perpendicular line to the boundary line that goes through the center.
  2. Consider the intersection of this line with the boundary line.
  3. Calculate the coordinates of the center and the intersection point. To calculate the coordinates we have to use the orders Abscissa(x) and Ordinate(y) in the menu Measure.

  4. Calculate the second coordinate of the point of the circumference that is in the perpendicular line. To make it we use the formula of the distance between two points. As the hyperbolic line is a vertical line, the point t that we have to consider in the double reason is the point of the infinite. If we designate for r the given radius we have that the formula to apply is: r = ln(u,v,s,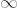infinite) where u is the center of the hyperbolic circumference, v the point which we want to construct and s the foot of the perpendicular. When we write the formula in the complexes, substitute the formula of the double reason and isolate s we obtain that the second coordinate is: ((u2-s2)/er)+s2. So, we put this formula in Calculate of the menu Measure to obtain the value.
  5. Create the point that belongs to the perpendicular line and that is at a distance given by the radius from the center. To create this point we use the order Plot As (x,y) in the menu Graph. This tool allows us to create a point if we have two selected values, these values will be the coordinates x and y. We take as x the first coordinate of the center and as y the second coordinated of the point obtained in the former step. Now, we have a point that it is at a distance given by the radius of the center. To find the other points we have follow a procedure as we did to demonstrated that given a point an a measure we can always draw a circumference with center in the point and radius the distance. We construct the other point that belongs to the perpendicular line and in the circumference considering the homothety with center in the foot of the perpendicular, s, and reason vs/us.
  6. Calculate the Euclidean distance between the points v and s and u and s.
  7. From the formula of the homothety we calculate zs, the Euclidean length of the segment ending in the foot of the perpendicular and in the point we obtain transforming the center by the homothety.
  8. Calculate the y coordinate of z adding up the y coordinate of s to the value obtained in the former step. We have to make it since we cannot assure that the point s belongs in the coordinated axis. We can obtain this calculation from the formula of the Euclidean distance between two points. In this case, it is simplified since the points v and z have equal the first coordinate. Then d(z,s)=|zy-sy|. To assure that we can always take out the absolute value it is only necessary to observe that the point s belongs to the boundary line and so, every point in the model have the second coordinate bigger than s. We can assure that the point z is in the model since we have obtained this point from another point in the model by a homothety with center in the boundary line and positive reason.
  9. Construct this second point of the circumference selecting the values of the second coordinate of the center and the one obtained in the former step and using the same tool as in the step (5).
  10. Mark the Euclidean midpoint of the segment ending in the two points of the hyperbolic circumference we have just constructed.
  11. With the former point as a center we plot the Euclidean circumference that passes through one of this points. This is the hyperbolic circumference we wanted to construct.
    12.

This construction gives us the hyperbolic circumference with center in the given point and radius the given measure since all steps can be made and with this construction we obtain a hyperbolic circumference.

List of tools
Hyperbolic geometry