Hyperbolic
Horocycle
In
the Half-Plane model of the Hyperbolic
Geometry, a horocycle is either an Euclidean line parallel to the
boundary line or a circumference tangent to the boundary line. This
construction will give us both
horocycles, that passes through a fixed point. To make the construction
we will think a horocycle as the the limit of a hyperbolic
circumference when its radius tends to infinity. Then, we will need two
points, one will be the hyperbolic center
of the circumference and the other the point in the horocycle.
- Plot the hyperbolic circumference that has center in the
first given point and passes through the second.
- Plot the Euclidean parallel line to the boundary line that
passes
through the second point. This line is one of the horocycles.
- Plot the perpendicular to the boundary line that passes
through the center of the hyperbolic
circumference in (1).
- Construct the intersection between the perpendicular line in
(3) with the boundary line.
In the following steps we will plot the Euclidean perpendicular
bisector to the
segment determined by the second fixed point and the intersection in
(4). To trace the perpendicular bisector we will follow the same
steps we made in the constructions we need it:
- Plot the Euclidean segment with endpoints in the
second fixed and in the intersection in (4).
- Plot its Euclidean midpoint.
- Construct the Euclidean perpendicular line to
the segment that passes through the midpoint.
This line is the Euclidean perpendicular bisector.
- Construct the intersection between the perpendicular
bisector and the perpendicular line in (3).
- Plot the Euclidean circumference with center in intersection
(8) and passes through the second fixed point.
This is the other horocycle.
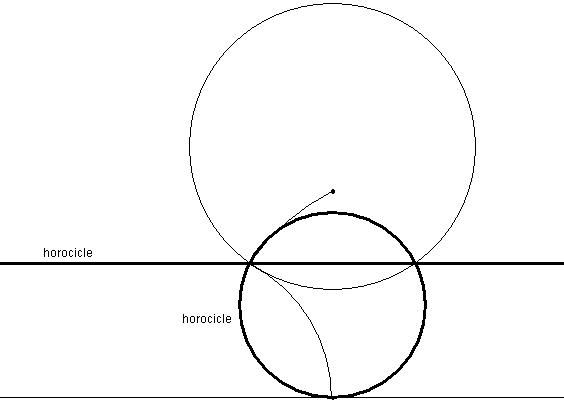
Observe we can see what we have named as horocycles fulfill
the definition. If we drag the center
of the hyperbolic circumference for the perpendicular in (3) towards
the boundary line we will obtain the second constructed horocycle and
if we drag it in the other direction we will obtain the first
constructed horocycle. However, notice that if we reproduce this
construction the circumference tangent to the boundary line will not be
plotted. This is because, it is used the circumference given the center
and a point tool and this tool had been constructed to plot a
circumference if and only if all of its points are hyperbolic.
List of tools
Hyperbolic
geometry