 Hyperbolic line
Hyperbolic line
The
hyperbolic lines, in the Poincaré's Half-Plane Model, are the
semicircumferences centered at a point of the boundary line and
arbitrary radius and the euclidian lines perpendicular to the boundary
line. In
this model these two objects are considered as lines so that
the concept of geodesics (the curve that minimizes the distance
between two points) still remain true.
The
hyperbolic line tool we have
constructed only allows us to draw the hyperbolic lines that are
semicircumferences. This restriction is because, in the construction we
use an intersection that does not exist when the hyperbolic line is
also an euclidean line.
Let's
see how we have constructed the tool when you have two points in the
allowed position:
- Draw the
Euclidean segment ending in the two given points.
- Construct
the midpoint.
- Draw the
perpendicular line that contains the segment of (1)
and that passes through the midpoint.
- Consider the
intersection of the constructed perpendicular line and the boundary
line. This point of intersection will be the center of the
circumference, which will give us the hyperbolic straight line. (This
is the intersection that does not exist when the two given points are
in the same perpendicular line.)
- Construct
the circumference with center at the last intersection
and that passes through one of the two given points.
- Mark the
intersection of this circumference with the boundary line.
- Plot the
arc of circumference with endpoints in the intersections of (7) and
passes through one
of the given points. This semicircumference is the hyperbolic line that
goes through the two fixed points.
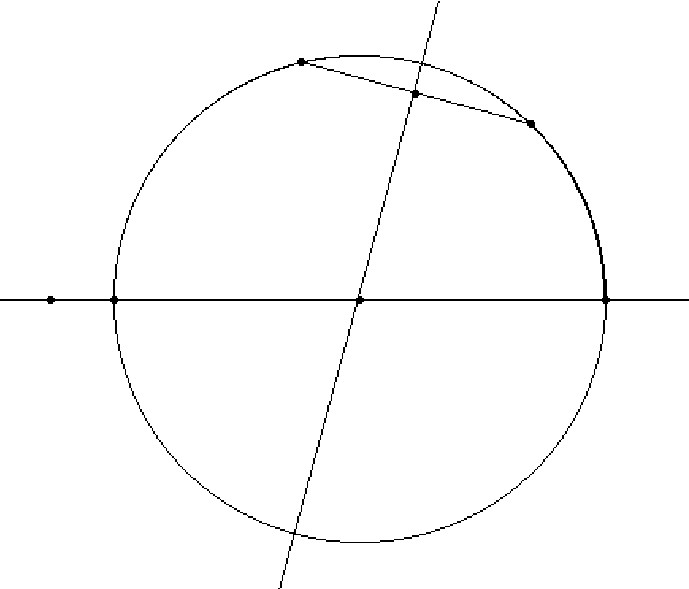 Some steps in the
construction of a hyperbolic line.
Some steps in the
construction of a hyperbolic line.
This construction allows us to find
the hyperbolic line. In the steps (2) and (3) we construct the
geometric place of the points of the plane that are equidistant of the
two points given, that is, the perpendicular bisector. Therefore, the center of the
circumference that we search is on this line but also
has to be on the boundary line, by definition of
hyperbolic straight line. Thus, on step (4), the center of the
circumference is determinated.
To get that the sketch only shows the
semicircumference we hide, with the hidden tool,
all other objects that we have constructed.
List of tools
Hyperbolic geometry
 Hyperbolic line
Hyperbolic line Hyperbolic line
Hyperbolic line Some steps in the
construction of a hyperbolic line.
Some steps in the
construction of a hyperbolic line.