 Perpendicular
bisector and midpoint
Perpendicular
bisector and midpoint
As
in
the
Euclidean case the hyperbolic perpendicular bisector is the geometric
place of the points of the plane that are equidistant
of two given points.
To construct the hyperbolic perpendicular bisector we
will use that the inversions with center in a point of the boundary
line are isometries for this model.
The midpoint of a segment is the point that belongs to the segment
and equidists of each endpoint.
Therefore, the midpoint is a point of the perpendicular bisector, in
fact, the intersection of the perpendicular bisector
with the segment. That is why we make an only
construction for both objects.
We will follow the following steps:
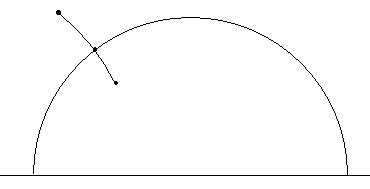
- Construct the hyperbolic segment
from the two given
points, C
and D.
- Plot the Euclidean line that goes through both
points.
- Consider the intersection of this line with the boundary
line. We designate this point for P.
- Plot the circumference of center P
and radius √(d(P,C).d(P,D)). This circumference
will be considered as the
inversion circumference.
- Consider the intersection between this circumference and the
boundary line.
- Consider the intersection between this circumference and the
hyperbolic segment constructed in the first step.
- Plot the arc of circumference that passes through an
intersection of the fifth step, the intersection of the sixth step and
the
other intersection of the fifth step.
We affirm that this arc of circumference is the hyperbolic
perpendicular bisector and the intersection point of the sixth step is
the hyperbolic midpoint of the given hyperbolic segment.
To prove that this construction really gives us the perpendicular
bisector and the hyperbolic
midpoint,
it is
necessary to prove that the distance between one of the given points
and the point that we suppose midpoint it is the same that the
distance between the other given point and the midpoint.
As the isometries preserve the distances we have that these two
distances
are equal if there is an inversion with center to the boundary line
that transforms one of the given points in the other one and leaves
fixed the created point. But this inversion is
precisely the circumference that we have constructed in fourth step
since it
has center in the boundary line, goes
through the midpoint (we have constructed the midpoint from the
intersection of this circumference) and exchange the given points. The
last affirmation is true because we have that both points are lined up
with the center
of the circumference, for construction, and the square of the radius of
the inversion circumference is
precisely the product of the
distance from the center, P,
in each point. So, the
intersection point of the sixth step is the midpoint.
Moreover, we have that all the points of the arc plotted in seventh
step are points of the perpendicular bisector since all the
points of the arc are at the same distance from the two given points.
This is because the same inversion brings the first point to the second
and fixes all the points of the perpendicular bisector.
List of tools
Hyperbolic
geometry