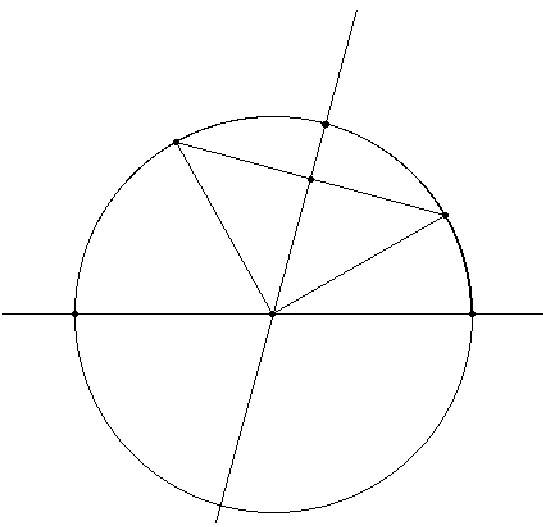
It is also necessary that the
intersection point that belongs in the same half-plane that the given
points will be
between these two given points. That is, if we follow the arc in the
order that indicates the step (3) we find the points in the indicated
order. Suppose that it is not
true. In general, every line divides the plane in two parts. We can
draw the lines that joins the
center with one of each given points. If our assumption is not true one
of these two lines will separate the intersection point and the other
given point. But it is not possible
because the intersection point is at the same distance from the two
given points and in this situation it is not possible. Thus, we will be able
to make this construction
whenever the given points do not belong to
the same line perpendicular to the boundary line. Finally, we only have
to hide all the constructed objects except the last arc.
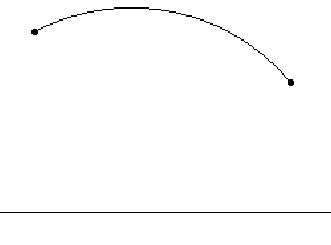
 Hyperbolic segment
Hyperbolic segment
