 Parallel lines
Parallel lines
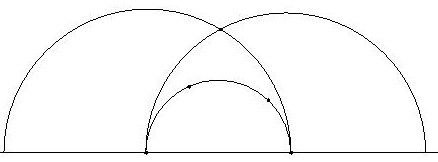
In
Hyperbolic Geometry, there are infinite lines that go
through an exterior point to a line and do not cut this line.
Of all these lines we considered that two are parallels with the given
line.
In order to use this tool, it will be necessary to give three points.
The
two first points we will consider that belong to the line and the third
will be the exterior point to the line.
We will suppose that the two first points are not in the same
perpendicular Euclidean line.
So, in this situation we will be able to construct the two parallel
lines easily.
- Plot the hyperbolic line that goes
through the
two first given points.
- Consider the two intersection points between this
circumference and the boundary line.
- Plot the hyperbolic line that goes through the exterior
point and one of the former intersections. This is one of
the two parallel lines.
- Plot the hyperbolic line that goes through the exterior
point and the other intersection.
This hyperbolic line is the other one.
This construction is correct whenever the exterior point does not
belong
to any perpendicular line to the boundary line going through one of the
intersection points. In this case we will not be able to plot
the hyperbolic line that goes through these two points. In the other
cases we obtain the parallel lines because they
fulfill that they cut the given line in a point of the boundary line
and this is the definition that we
consider of parallel lines.
List of tools
Hyperbolic geometry
 Parallel lines
Parallel lines