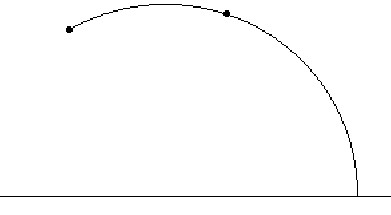
 Hyperbolic ray
Hyperbolic ray
To construct a
hyperbolic ray we need two ordered points. The order we fix the
two points is important since we will consider that the hyperbolic ray
has the origin in the first
given point.
Because of that, to construct a hyperbolic ray with the Sketchpad we have to have in
account that the order with which the points are marked will be the
order that we will use, that is, the first marked point will be
the origin of the ray.
Let's see the steps
followed to construct a ray:
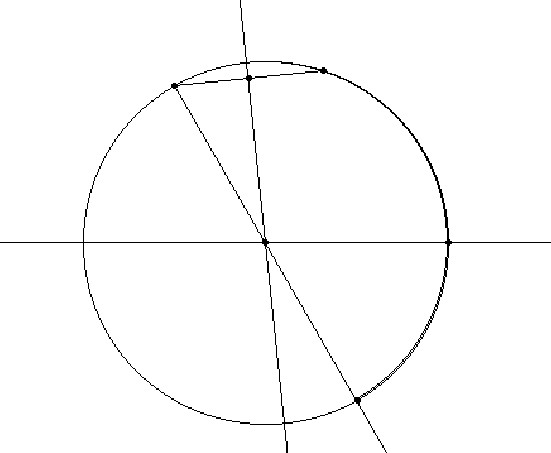
- Draw the
circumference that passes through the two given points and has the
center on the boundary line repeating the five first steps followed to
construct the hyperbolic line.
- Draw the
Euclidean line through the first point and the center of the
circumference.
- Consider
the intersection of this line and the circumference. There
are two points of intersection since the line we have
constructed is a prolongation of a diameter of the circumference. One
intersection is the first given point. We will need the other
intersection point.
- Construct
the arc of circumference that has origin in the first given point,
goes through the second given point and finishes in the intersection of
the former step.
- Consider
the intersection of the arc of the former step with the boundary line.
This point, lying in the boundary line, will give us where the
hyperbolic ray finishes.
- Draw
the arc of circumference that joins the first given point, passes
through the second and finishes in the intersection point considered at
(5).
This arc of circumference is the hyperbolic ray we wanted to
construct.
If we prove that step (4) is well defined
in any situation we will have proved that this construction is correct.
This is true because the
point we suppose that will always be the third is the antipodal point of the first given point and, to
be the antipodal, will be on the other half of the plane
determined by the boundary line. The two given points will always be on
the same half of the plane since they are
hyperbolic points. So, we will always be able to make this construction
and we will always obtain the ray in
the correct direction.
Once made the construction it is only necessary to hide all objects
except the last arc of circumference.
List of tools
Hyperbolic
geometry

 Hyperbolic ray
Hyperbolic ray
