Hyperbolic
triangle
As in the
Euclidean case, a hyperbolic triangle, is determinated by
three points not lying in the same line.
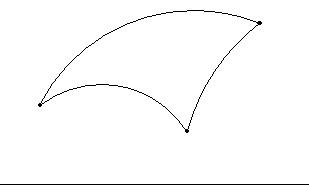
To form a triangle we have to join
this three points, in pairs, by segments. As the tool that allows us to
construct segments is only defined when the endpoints do not belong to
the same Euclidean line
perpendicular to the boundary line, we will suppose
that the three points that describe us the triangle are not in this
situation.
We could think that if two points are in the last situation they
can be joined by an
Euclidean segment since this Euclidean segment and the hyperbolic
segment coincide, but we can
not make this if we want the constructions
to be interactive since in this case the Euclidean segment will
continue
being Euclidean and it will not be converted into an arc of
circumference.
So, to construct a hyperbolic
triangle, it is only necessary to open a new Sketch, draw the boundary line from
two points A and B and fix three points in the allowed
position. Now, with the hyperbolic segment tool
we draw the three
sides of the triangle.
List of tools
Triangles
Hyperbolic geometry