Circumferència hiperbòlica: centre i radi

Donat un punt i una distància sempre podem construir una circumferència hiperbòlica que té el centre en aquest punt i radi la distància. A Taller de Geometria Hiperbòlica.pdf hem vist el mètode per construir-la. Els passos que hem seguit per construir una circumferència hiperbòlica donat el centre i el radi es basen en aquest mètode.

Per utilitzar aquesta eina necessitem fixar un sistema de coordenades. Aquest sistema el necessitem per donar coordenades als punts i poder utilitzar la fórmula que ens dóna la distància entre dos punts. Volem utilitzar aquesta fórmula ja que tenim el radi de la circumferència, és a dir, la distància entre el centre i qualsevol dels punts de la circumferència hiperbòlica. El sistema es fixa tot sol en triar l'eina.
Per poder-la utilitzar només necessitarem fixar, com sempre, la recta de l'infinit, el punt que volem que sigui el centre i el radi. Primer de tot cal escriure la longitud del radi amb l'opció Measure/Calculate. Després, marcar el punt i la mesura del radi que haguem escrit. Una vegada tenim aquests objectes ja podem seguir els següents passos:

  1. Tracem la recta perpendicular que passa pel centre.
  2. Considerem la intersecció d'aquesta recta amb la recta de l'infinit.
  3. Calculem les coordenades del centre i del punt d'intersecció. Per calcular les coordenades hem d'utilitzar les comandes Abscissa(x) i Ordinate(y) dins del menú Measure.

  4. Calculem la segona coordenada del punt de la circumferència que està a la recta perpendicular. Per fer-ho utilitzem la fórmula de la distància entre dos punts. Com que la recta hiperbòlica és una recta vertical, el punt t que hem de considerar de la raó doble és el punt de l'infinit. Si designem per r el radi donat tenim que la fórmula a aplicar és: r = ln(u,v,s,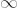infinit) on u és el centre de la circumferència hiperbòlica, v el punt que volem construir i s el peu de la perpendicular. Passant la fórmula als complexos, aplicant la fórmula de la raó doble i aïllant obtenim que la segona coordenada ve donada per: ((u2-s2)/er)+s2. Així doncs, posem aquesta fórmula a la comanda Calculate del menú Measure.
  5. Creem el punt que pertany a la recta perpendicular i que està a una distància igual que el radi. Per crear aquest punt utilitzem la comanda Plot As (x,y) del menú Graph. Aquesta eina ens permet crear un punt si tenim seleccionats dos valors que seran la x i la y. Prenem com a x la primera coordenada del centre i com a segona l'obtinguda en el pas anterior. Ara ja tenim un punt que està a la distància determinada pel radi del centre. Per trobar els altres punts hem seguit un procediment semblant al que ens ha permès demostrar que donat un punt i una distància sempre podem pensar que aquest punt és el centre d'una circumferència que té per radi la distància. Construïm l'altre punt que pertany a la recta perpendicular i està a la distància determinada pel radi del centre. Per construir aquest punt cal considerar l'homotècia de centre el peu de la perpendicular, s, i raó vs/us.
  6. Calculem la distància euclidiana entre els punts v i s i u i s.
  7. A partir de la fórmula de l'homotècia calculem zs, la longitud euclidiana del segment que uneix el punt que obtenim de transformar el centre per la homotècia i el peu de la perpendicular.
  8. Calculem la coordenada y de z sumant la coordenada y de s al valor obtingut al pas anterior. Això ho hem de fer perquè en el pas anterior hem obtingut la distància entre els dos punts i aquest valor només coincideix amb el de la coordenada y si el punt s està a l'eix de les x cosa que no podem assegurar ja que l'eix no el fixem nosaltres. L'operació que fem a aquest pas l'obtenim de la fórmula de la distància euclidiana entre dos punts. En aquest cas, se simplifica molt ja que els punts v i z han de tenir igual la primera coordenada. Llavors d(z,s)=|zy-sy|. Per assegurar-nos que sempre podem treure el valor absolut només cal observar que el punt s pertany a la recta de l'infinit que hem fixat per aquest model del semiplà, per tant, qualsevol altre punt del model tindrà segona coordenada més gran. Podem assegurar que el punt z, que hem obtingut a partir de l'homotècia de centre un punt de la recta de l'infinit i raó positiva sempre transforma punts del semiplà en punts del semiplà i el punt u és, per ser el centre d'una circumferència hiperbòlica, del semiplà.
  9. Construïm aquest segon punt de la circumferència seleccionant els valors de la segona coordenada del centre i l'obtingut en el pas anterior i utilitzant la mateixa eina que en el pas (5).
  10. Marquem el centre euclidià del segment d'extrems els dos punts de la circumferència hiperbòlica que hem construït.
  11. Amb el punt anterior com a centre tracem la circumferència que passa per un d'aquest punts. Aquesta és circumferència hiperbòlica que volíem construir.

Aquesta construcció ens dóna la circumferència hiperbòlica que té per centre i radi els escollits per l'usuari ja que tots els passos es poden fer i amb aquesta construcció obtenim una circumferència hiperbòlica.

Llista d'eines
Geometria hiperbòlica