Horocicle
hiperbòlic
Sabem que
l'horocicle, en el model del semiplà de Poincaré de la
Geometria Hiperbòlica, és una recta euclidiana
paral·lela a la recta de l'infinit que passa pel punt de la
circumferència que hem fixat o una circumferència
hiperbòlica
tangent a la recta de l'infinit que passa pel punt (i té el
centre
sobre la recta perpendicular en la que el desplacem). En aquesta
construcció farem els dos horocicles. Necessitarem dos punts, un
serà el centre hiperbòlic de la circumferència i
l'altre el punt
de la circumferència a partir del qual volem traçar els
horocicles.
- Tracem la circumferència
hiperbòlica que té centre
en el
primer punt donat i passa pel segon.
- Tracem la recta paral·lela (en el sentit
euclidià) a la
recta
de l'infinit que passa pel segon punt. Aquesta recta és un dels
horocicles.
- Tracem la perpendicular a la recta de l'infinit que passa
pel
centre de la circumferència hiperbòlica traçada a
(1).
- Construïm la intersecció de la recta
perpendicular del pas
anterior amb la recta de l'infinit.
En els següents passos tracem la mediatriu euclidiana al
punt
fixat i a la
intersecció anterior. Seguirem els mateixos passos que en totes
les altres construccions que la necessitem:
- Tracem el segment euclidià entre el punt
fixat de la
circumferència
de (1) i la intersecció anterior.
- Tracem el punt mig euclidià del segment anterior.
- Construïm la recta perpendicular euclidiana al segment
pel punt
mig.
Aquesta recta és la mediatriu.
- Construïm la intersecció entre la mediatriu i la
recta
perpendicular traçada a (3).
- Tracem la circumferència euclidiana que té com
a centre
la
intersecció anterior i passa pel punt fixat. Aquest és
l'altre
horocicle.
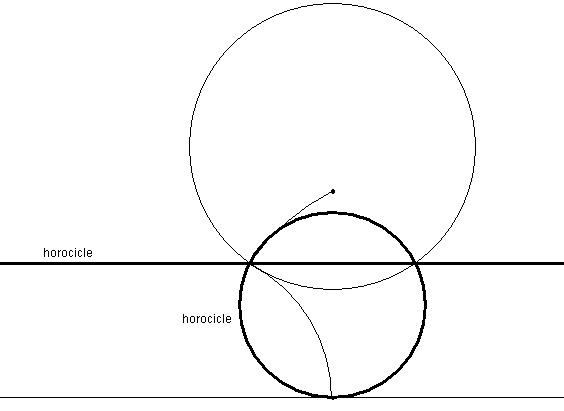
Observem que podem veure com realment els dos llocs geomètrics
que
hem anomenat horocicles en compleixen la definició. Si movem el
centre de la circumferència hiperbòlica per la recta
perpendicular
a la recta de l'infinit que passa pel centre, primer en un sentit
i després en l'altre, obtindrem que la circumferència
s'aproxima,
en un cas, a la recta traçada al pas (2) i, en l'altre, a la
circumferència tangent. Cal observar, però, que la
circumferència
tangent no la construeix ja que, en el moment en què fem que la
circumferència hiperbòlica talli la recta de l'infinit
aquesta
desapareix. Això ja és coherent amb la definició
del model;
considerem que els punts de la recta de l'infinit no són punts
del
model.
Llista d'eines
Geometria
hiperbòlica