 Mediatriu
i punt mig hiperbòlics
Mediatriu
i punt mig hiperbòlics
Com en el cas
euclidià la mediatriu hiperbòlica és
el lloc
geomètric dels punts del pla que equidisten de dos punts donats.
Per construir la mediatriu hiperbòlica utilitzarem que les
inversions amb centre un punt de la recta de l'infinit són
isometries per aquest model.
El punt mig d'un segment és el punt que pertany al segment
determinat pels dos punts i que equidista d'ells. Per tant, el punt mig
és un punt de la mediatriu, de fet, la intersecció
de la mediatriu amb el segment. Per això fem una única
construcció pels dos objectes.
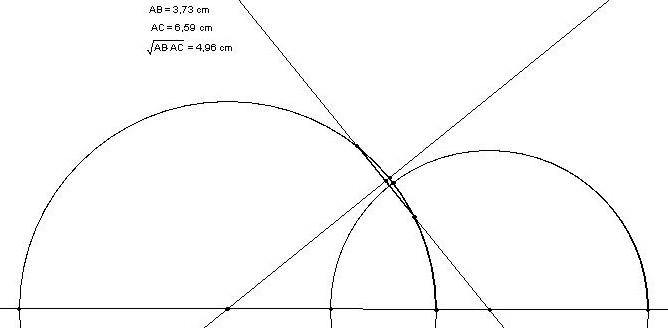
Seguirem els següents passos:
- Construïm el segment
hiperbòlic a partir dels
dos punts
donats, C i D.
- Tracem la recta euclidiana que passa pels dos punts.
- Considerem la intersecció d'aquesta recta amb la
recta de
l'infinit. Designem per P
aquest punt.
- Tracem la circumferència de centre P i radi
√(d(P,C).d(P,D)). Aquesta circumferència serà
considerada
com a circumferència d'inversió.
- Considerem la intersecció d'aquesta
circumferència amb la
recta de l'infinit.
- Considerem la intersecció d'aquesta
circumferència amb el
segment hiperbòlic construït a (1).
- Tracem l'arc de circumferència que passa per una
intersecció
del pas (5), la intersecció del pas (6) i l'altra
intersecció del
pas (5).
Afirmem que l'arc de circumferència de (7) és la
mediatriu
hiperbòlica i el punt d'intersecció del pas (6) el punt
mig
hiperbòlic del segment hiperbòlic determinat pels dos
punts B i C.
Per provar que aquesta construcció realment ens dóna la
mediatriu
i el punt mig hiperbòlics cal provar que la distància
entre un
dels punts donats i el punt que suposem punt mig és la mateixa
que
la distància entre l'altre punt donat i el punt mig.
Com que les
isometries conserven les longituds tenim que aquestes dues
distàncies són iguals si existeix una inversió amb
centre a la
recta de l'infinit que transforma un dels punts donats en l'altre
i deixa fix el punt que hem construït al pas (6). Però
aquesta
inversió és precisament la donada per la
circumferència que hem
construït al pas (4) ja que té centre a la recta de
l'infinit,
passa pel punt mig (hem construït el punt mig a partir de la
intersecció d'aquesta circumferència) i transforma els
punts
donats entre ells. L'última afirmació és certa
perquè tenim que
els dos punts estan alineats amb el centre de la circumferència,
per construcció, i el radi al quadrat de la
circumferència
d'inversió és precisament el producte de la
distància del centre, P,
a cada un dels dos punts. Així doncs, el punt
d'intersecció
del pas (6) és el punt mig.
A més, tenim que tots els punts de l'arc traçat al pas
(7) són
punts de la mediatriu ja que tots els punts d'aquest estan a la
mateixa distància dels dos punts donats. Això és
perquè la mateixa
inversió porta el primer punt al segon i deixa fixos els punt de
la mediatriu.
Per tal que només ens mostri la mediatriu o el punt mig cal que
amaguem tots els altres objectes que hem construït. D'aquesta
manera el resultat final que veiem és el següent.
Llista d'eines
Geometria
hiperbòlica