Optimisation 2015/16
Master's degree in Modelling for Science and Engineering
Combinatorial Algorithms for graphs
- General definitions and searches on graphs
- Dijkstra Algorithm for optimum paths on graphs
- A* Algorithm: Heuristic search for optimum paths on graphs
Assignments:
- Dijkstra Algorithm (recommended):
- Solve the project proposed here.
- A* Algorithm (compulsory):
- Routing problem: Barcelona-Sevilla; the data map of spain can be downloaded from
here (348.5Mb).
For testing the program, you can use the much smaller file catalunya.csv.zip (51.9Mb)
(it has only 3472620 nodes and 201235 ways and it has the same format as the file
spain.csv.zip).
Valid nodes ID for start and goal are: 771979683 (in Girona) and 429854583 (in Lleida).
Overview of optimization algorithms: Deterministic and heuristic
Deterministic optimization for nonlinear problems (constrained and non-constrained)
- Gradient descent ("steepest descent")
- Newton and Quasi-Newton methods
- Conjugate gradient methods
- Levenberg Marquardt
- Karush-Kuhn-Tucker conditions for constrained optimization
- Penalty and Barrier Methods for constrained optimization
Assignments:
Solve the problems proposed here.
Genetic Algorithms
Assignments:
- First exercise (compulsory part): The traveling salesman problem
- A traveling salesman must visit all cities appearing in the
table of distances between European cities
starting and ending in Barcelona. He travels by car. Use a GA to compute the optimum route according to driving distance.
Se also the "ad-hoc" crossover operations above.
- Second exercise (optional part):
Maximization of a (complicate and artificial) function by a genetic algorithm
Simulated Annealing
- Basic bibliography
- Some interesting links from the wikipedia page
Assignment (based on the last previous link)
You are a zookeeper in the reptile house.
One of your rare South Pacific Tufted Wizzo lizards (Tufticus wizzocus) has just had EIGHT babies.
Your job is to find a place to put each baby lizard in a nursery.
However, there is a catch, the baby lizards have very long tongues.
A baby lizard can shoot out its tongue and eat any other baby lizard before you have time to save it.
As such, you want to make sure that no baby lizard can eat another baby lizard in the nursery (burp).
For each baby lizard, you can place them in one spot on a grid.
From there, they can shoot out their tongue up, down, left, right and diagonally as well.
Their tongues are very long and can reach to the edge of the nursery from any location.
Figure 1 shows in what ways a baby lizard can eat another.
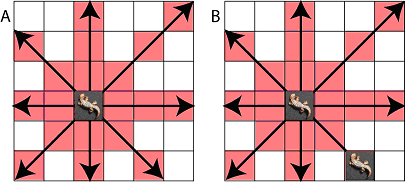 |
|
Figure 1 (A) the baby lizard can attack any other lizard in a red square. Thus it can be seen that a baby lizard can eat another lizard to its top, bottom, left right or diagonal. (B) In this setup both lizards can eat each other.
|
In addition to baby lizards, your nursery has some trees planted in it.
Your lizards cannot shoot their tongues through the trees nor can you move a lizard into the same place as a tree.
As such, a tree will block any lizard from eating another lizard if it is in the path.
Additionally, the tree will block you from moving the lizard to that location.
Figure 2 shows some different valid arrangements of lizards
 |
|
Figure 2 Both nurseries have valid arrangements of baby lizards such that they cannot eat one another.
(A) with no trees, no lizard is in a position to eat another lizard.
(B) Two trees are introduced such that the lizard in the last column cannot eat the lizard in the second or fourth column.
|
Write a program in C that will take as input the number (from 0 to 8) and positions of trees in the grid,
and returns a valid configuration for the 8 baby lizards computed by using simulated annealing.
Idea of the algorithm:
The lizards are initially placed in random rows and columns such that each lizard is in a different row and a different column.
During each turn, an attacked lizard is chosen and a random column is picked for that lizard.
If moving the lizard to the new column will reduce the number of attacked lizards on the board, the move is taken
(so the energy function is the number of attacked lizards).
Otherwise, the move is taken only with a certain probability, which decreases over time.
Questions to be addressed in the report
- Why is simulated annealing a good algorithm for this problem? (think about complexity and other considerations).
- What would be reasonable temperature decrease schedules to use for this problem? Include equations and function graphs for each schedule that you test.
- Experiment with the different temperature schedules you found and conduct a comparative analysis, running your algorithm on different problems (that is, different number and positions of trees).
Motivate your answer with a table showing some measure of performance on your test problems (for example, steps taken) for your different schedules.
Include a conclusion on which schedule seems superior with supporting statistics and illustrations.
- In addition to using simulated annealing, could you also have used genetic algorithms to solve this problem? If so, how would you have done it (just explain, you do not have to code), if not, then why?
Ant colony algorithms
Concrete Examples
Assignments
Solve the traveling salesman problem stated in Genetic Algorithms by using an Ant Colony System.
Take edge probabilities of the form stated in page 249 of the [Dorigo, Blum] paper.
Evaluation
The list of assignments that will be proposed is the following:
| Assignment |
Status |
Deadline |
Weight in the final mark |
| Map routing (A* algorithm) |
Compulsory |
11/01/2015 |
40% |
| Deterministic Optimisation |
Compulsory |
February 28, 2015 |
30% |
| Genetic Algorithm |
Compulsory |
February 28, 2015 |
30% |
| Dijkstra Algorithm |
Optional |
February 28, 2015 |
Together increment the final mark up to 20% |
| Genetic Algorithm (2nd) |
| Simulated Annealing |
| Ant Colony Algorithm |
- For each assignment a report must be written including:
- introduction stating the problem and the algorithm to solve it,
- the code of the program,
- the results of running the program and
- conclusions.
- The quality of the code of the program will be taken into account for the marks of the assignments and discussed in the interviews.
