Angle
of parallelism
The
angle of parallelism has an important role in the Hyperbolic
Geometry since it relates lengths and angles. In Euclidean Geometry it
is not possible to find any similar relation.
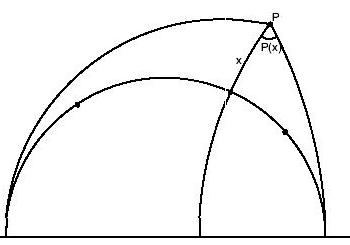
To describe the angle of parallelism we need to fix a line, r, and an
exterior point
P. Then, we consider the perpendicular line to r that passes through P and its intersection, Q, with r.
The length of the segment PQ coincides
with the distance from P to r. Now, we
consider the two parallel lines to r
that contains P and the angle
between one of these parallel lines and the perpendicular line. This
angle is defined as the angle of parallelism.
We have two tools to calculate the angle of parallelism. One of them
only calculates the angle of parallelism without making any apparent
modification in the construction and the other one, apart from
calculating
its value, represents this angle and draws the
two parallel lines.
For both cases we need three ordered points, so that the two first
belong to the line. Now, we
calculate the value of the angle of parallelism:
- Construct the hyperbolic line that
joins the two first
points.
- Plot the parallel lines.
Now, we calculate the value of the angle of parallelism from the
Euclidean angle since in this model the hyperbolic angles coincide with
the Euclidean ones.- Plot the tangent line to the two
Euclidean circumferences that define each one of the
parallel line containing the outer point.
- Calculate the Euclidean angle between the two lines in (3).
This angle measure twice the angle of
parallelism.
- Divide the last measure by two. This is the
value of the angle of
parallelism.
We hide all objects except from the result of the step (5).
If we want to draw the bisector it is necessary to go
on with the following steps
and not to hide any of the former objects.
- Plot the two hyperbolic segments
that have as an endpoints the
outer point and the intersection point of the line given with the
boundary line. In fact, these two
hyperbolic segments that we have constructed are not hyperbolic
segments (they have a point in the boundary line) but we want these
segments to plot the arc of circumference
that joins both points, so we can use this construction.
- Plot the hyperbolic angle bisector
of the angle between the two
former segments. Observe that we can think each segment as a hyperbolic
ray.
- Consider the intersection point of the hyperbolic
angle bisector with the line in (1).
- We plot the hyperbolic segment
that joins the two former
points. This is the segment that defines the angle of parallelism.
Observe that the step
(9) cannot be made in any situation. If the hyperbolic segment is also
a
Euclidean segment we cannot construct it with the hyperbolic segment
tool. If
it is the case, drag some of the initial points so that in the new
position the segment could be
constructed.
List of tools
Hyperbolic
geometry

