Hyperbolic
circumference: three points
We
can also plot the circumference that goes through three given points.
This construction will not always be possible to be done since not
always, given three points, there is a hyperbolic circumference that
contains them, as we proved in Workshop
of Hyperbolic Geometry.pdf
(in Catalan). Anyway, if it exists
it is unique.
To construct it, it is necessary to fix three points of the half-plane
model. The steps that we have followed are
the following ones:
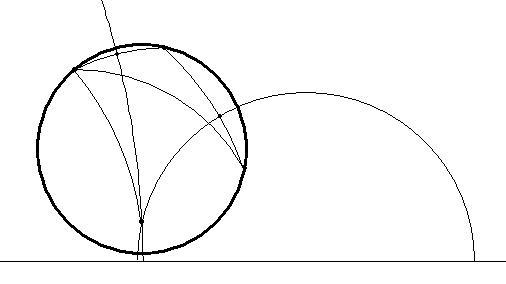
- Plot the hyperbolic triangle that joins the three given
points. We can construct it plotting the three hyperbolic
segments. Anyway, we have created a
tool that allows us to construct the hyperbolic
triangle given
three points.
- Plot the hyperbolic perpendicular
bisector for two of the three segments.
- Consider the intersection of these two.
- Plot the hyperbolic circumference
with center in the former intersection point and goes through one of
the three given
points.
This is the hyperbolic circumference which we want to construct.
This construction, as we have
commented, will not always be possible. The step that will fail will be
the third. The perpendicular bisectors will not cut in the half-plane.
In this case, no circumference will be constructed
since in the sketch of the hyperbolic perpendicular bisector we only
draw the semicircumference that belongs to
the half-plane. So, the construction will
detect correctly when it is not possible to construct the hyperbolic
circumference that goes through three given points.
List of tools
Hyperbolic
geometry