Optimisation 2020/21

Master's degree in Modelling for Science and Engineering

C learning

Combinatorial Algorithms for graphs

  • General Bibliography

    • Compulsory Assignment

    A* Algorithm:
    Routing problem: Barcelona-Sevilla; the data map of spain can be downloaded from here (348.5Mb).
    For testing the program, you can use the much smaller file catalunya.csv.zip (51.9Mb) (it has only 3472620 nodes and 201235 ways and it has the same format as the file spain.csv.zip). Valid nodes ID for start and goal are: 771979683 (in Girona) and 429854583 (in Lleida).
    Here you can find my solution of the Barcelona-Sevilla problem for reference (recall that it depends globally on the distance formula). in the setting of the memory structure recommended in the assignment.

    Optional Assignment

    Dijkstra Algorithm:
    Solve and implement the solution of the example Flight Agenda in the document Dijkstra's Application.
    As data you can use the following two files (if you have already done the assignment with some other data, please do not continue reading):
    As assignment you can find the flight agenda for the following itineraries (all of them with departure at 9am):

    Heuristics and problem representation

    Overview of optimization algorithms: Deterministic and heuristic

    Deterministic optimization for nonlinear problems (constrained and non-constrained)

    Compulsory Assignment

    Solve the Rosenbrock’s function exercise.

    Genetic Algorithms

    Optional Assignment (to train the skills in a canonical-academic problem)

    Maximization of a (complicate and artificial) function by a genetic algorithm.

    Compulsory Assignment

    A Genetic Algorithm application for COVID-19 pandemic. You also need an efficiency aiming implementation of the Runge-Kutta-Fehlberg-Simo of orders 78 in Cnot++ (version 2.2).
    Note on 20210103: There have been a lot of changes in the file (in general improving the advice), but be aware that we have changed the figured real data (the new one agrees better with the discretization, and so it makes the exercise easier).

    Simulated Annealing

    Optional Assignment

    You are a zookeeper in the reptile house. One of your rare South Pacific Tufted Wizzo lizards (Tufticus wizzocus) has just had EIGHT babies. Your job is to find a place to put each baby lizard in a nursery. However, there is a catch, the baby lizards have very long tongues. A baby lizard can shoot out its tongue and eat any other baby lizard before you have time to save it. As such, you want to make sure that no baby lizard can eat another baby lizard in the nursery (burp).

    For each baby lizard, you can place them in one spot on a grid. From there, they can shoot out their tongue up, down, left, right and diagonally as well. Their tongues are very long and can reach to the edge of the nursery from any location. Figure 1 shows in what ways a baby lizard can eat another.

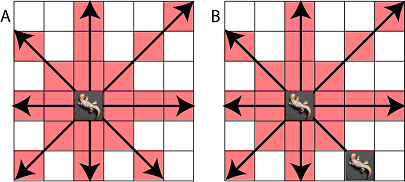    Figure 1 (A) the baby lizard can attack any other lizard in a red square. Thus it can be seen that a baby lizard can eat another lizard to its top, bottom, left right or diagonal. (B) In this setup both lizards can eat each other.

    In addition to baby lizards, your nursery has some trees planted in it. Your lizards cannot shoot their tongues through the trees nor can you move a lizard into the same place as a tree. As such, a tree will block any lizard from eating another lizard if it is in the path. Additionally, the tree will block you from moving the lizard to that location. Figure 2 shows some different valid arrangements of lizards

    Figure 2 Both nurseries have valid arrangements of baby lizards such that they cannot eat one another. (A) with no trees, no lizard is in a position to eat another lizard. (B) Two trees are introduced such that the lizard in the last column cannot eat the lizard in the second or fourth column.

    Write a program in C that will take as input the number (from 0 to 8) and positions of trees in the grid, and returns a valid configuration for the 8 baby lizards computed by using simulated annealing.

    Idea of the algorithm: The lizards are initially placed in random rows and columns such that each lizard is in a different row and a different column. During each turn, an attacked lizard is chosen and a random column is picked for that lizard. If moving the lizard to the new column will reduce the number of attacked lizards on the board, the move is taken (so the energy function is the number of attacked lizards). Otherwise, the move is taken only with a certain probability, which decreases over time.

    Questions to be addressed in the report

    1. Why is simulated annealing a good algorithm for this problem? (think about complexity and other considerations).
    2. What would be reasonable temperature decrease schedules to use for this problem? Include equations and function graphs for each schedule that you test.
    3. Experiment with the different temperature schedules you found and conduct a comparative analysis, running your algorithm on different problems (that is, different number and positions of trees). Motivate your answer with a table showing some measure of performance on your test problems (for example, steps taken) for your different schedules. Include a conclusion on which schedule seems superior with supporting statistics and illustrations.
    4. In addition to using simulated annealing, could you also have used genetic algorithms to solve this problem? If so, how would you have done it (just explain, you do not have to code), if not, then why?

    Ant colony algorithms

    Optional Assignment

    A traveling salesman must visit all cities appearing in the table of distances between European cities starting and ending in Barcelona. He travels by car. Use an ACO to compute the optimum route according to driving distance (take edge probabilities of the form stated in page 249 of the [Dorigo, Blum] paper).

    Evaluation

    The list of assignments that will be proposed is the following:
    Assignment Status Deadline Maximum mark
    (pass is more than 49 points)
    Map routing (A* algorithm) Compulsory January 10, 2021 50 points
    Genetic Algorithm Compulsory February 16, 2021 30 points
    Deterministic Optimisation Compulsory January 10, 2021 20 points
    Dijkstra Algorithm Optional February 16, 2021 Together increment the final mark up to 20 points
    Simulated Annealing
    Ant Colony Algorithm