Equidistant
hiperbòlica
Aquesta eina
està pensada per trobar l'equidistant de rectes
hiperbòliques que són semicircumferències
euclidianes. Això només
és perquè l'eina de recta
hiperbòlica només la tenim
definida en aquesta situació. De totes maneres el lector pot
crear
fàcilment l'eina pel cas en què la recta
hiperbòlica sigui també
euclidiana ja que, de fet, en els passos que explicarem per
l'altre cas haurem de traçar l'equidistant hiperbòlica
per una
recta perpendicular a la de l'infinit. Per construir l'equidistant
ens vam basar en la teoria que vam utilitzar per assegurar la seva
existència (Taller de Geometria
Hiperbòlica.pdf).
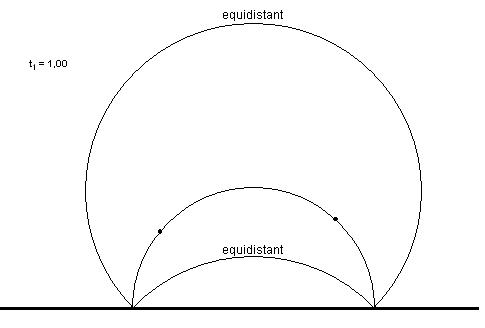
Per construir l'equidistant necessitem, a més
de la
recta de l'infinit, dos punts que ens determinaran la recta
hiperbòlica i una distància; la distància que
volem que
l'equidistant estigui de la recta hiperbòlica. Com que
utilitzarem
distàncies necessitarem fixar els eixos, però sabem
que el
resultat no ens dependrà d'on els haguem fixat.
Així doncs, els passos que seguim són els següents:
- Tracem la recta
hiperbòlica de la que volem
traçar
l'equidistant.
- Tracem la circumferència euclidiana que té el
centre en
un
dels dos punts d'intersecció de la recta hiperbòlica amb
la de
l'infinit i passa pel peu d'una de les perpendiculars que passen
per un dels punts donats. Aquesta serà la circumferència
que ens
determinarà la inversió a partir de la qual passarem la
recta
hiperbòlica a una recta perpendicular a la de l'infinit.
- Tracem la recta perpendicular a la recta de l'infinit que
passa pel punt d'intersecció de la circumferència
d'inversió i la
recta hiperbòlica. Aquesta és la recta que
obtindríem de la
inversió de la recta hiperbòlica.
- Tracem la circumferència
hiperbòlica amb
centre un punt
de la
recta perpendicular i radi la distància donada. Hem pres com a
centre el punt d'intersecció de la recta hiperbòlica
original amb
la circumferència d'inversió. D'aquesta manera assegurem
que la
circumferència hiperbòlica tallarà la recta
hiperbòlica original.
- Tracem les semirectes euclidianes amb origen a la
intersecció
de la recta perpendicular que hem obtingut al pas (3) amb la recta
de l'infinit i que passin pel punt d'intersecció de la recta
hiperbòlica original amb la circumferència
hiperbòlica traçada al
pas anterior. Aquestes dues semirectes són les equidistants a la
recta hiperbòlica del pas (3).
Només ens falta tornar a aplicar la inversió per retrobar
la recta
hiperbòlica original i les dues equidistants.
- Considerem les dues interseccions de les dues rectes
traçades
al pas anterior amb la circumferència que ens dóna la
inversió.
Aquests punts són fixos en fer la inversió.
- Tracem la circumferència euclidiana que s'obté
de
la inversió
d'una de les dues rectes traçades al pas (5). Per les propietats
de les inversions podem traçar la circumferència que
passa pels
dos punts d'intersecció obtinguts al pas anterior per aquesta
recta i pel centre de la inversió. Per traçar aquesta
circumferència no utilitzem l'eina que ens dóna l'arc per
tres
punts ja que volem la circumferència sencera perquè
després
voldrem considerar només l'arc que pertany al semiplà de
Poincaré.
Així doncs, cal que busquem el centre. Per fer-ho només
cal
considerar dos dels tres segments que obtenim en unir els tres
punts. Per aquests dos segments tracem la seva mediatriu. El punt
d'intersecció serà el centre. Aquesta construcció
la podrem fer
sempre ja que ara estem pensant amb Geometria Euclidiana.
- Considerem la intersecció de la circumferència
que hem
construït en el pas anterior amb la recta de l'infinit.
- Tracem l'arc de circumferència que té origen
en un dels
dos
punts anteriors, passa pel punt d'intersecció del pas (6) que
pertany al semiplà de Poincaré i acaba a l'altre punt
d'intersecció.
- Fem la mateixa construcció que en els tres passos
anteriors
però per l'altra recta. D'aquesta manera hem obtingut les dues
equidistants a la distància fixada a la recta hiperbòlica
donada.
Llista d'eines
Geometria
hiperbòlica