Transport
de segments
A la
Geometria Euclidiana sabem que hi ha unes aplicacions que tenen la
propietat de conservar les
distàncies i els angles. Aquestes aplicacions, que anomenem
isometries
són els girs i les translacions. Les isometries porten rectes a
rectes i segments d'igual
longitud a segments d'igual longitud. Per aplicar una d'aquestes
transformacions necessitem conèixer, en el cas de les
translacions la direcció i la distància o l'angle en el
cas dels girs.
A la Geometria
Hiperbòlica també tenim isometries. En el model del
semiplà de Poincaré les isometries són les
aplicacions que s'obtenen de composició d'inversios respecte
circumferències amb centre a la recta de l'infinit i radi
arbitrari. Per tant, per determinar-hi una isometria és
necessari fixar un punt a la recta de l'infinit (que serà el
centre de la circumferència d'inversió) i una
distància (que serà el radi de la circumferència
d'inversió).
A partir de les isometries podrem transportar els objectes de la
Geometria Hiperbòlica.
Aquest sketch permet transportar un segment a una altra posició
fixat el punt d'inici del segment transportat i la direcció,
és a dir, és necessari fixar un punt i un raig per
transportar un segment. Per fer el transport utilitzarem dues
isometries.
Per fer el transport d'un segment CD
al raig amb extrem E hem
seguit els passos següents:
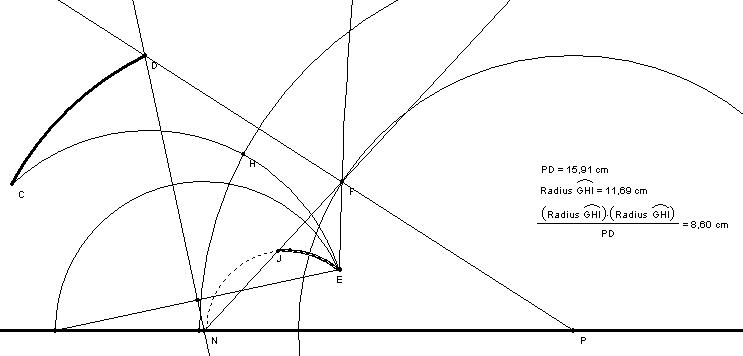
- Considerem
el segment hiperbòlic
CE.
- Tracem la mediatriu
hiperbòlica del segment hiperbòlic CE.
Considerem la
circumferència que determina la mediatriu com a
circumferència d'una inversió. Apliquem la
inversió als punts C i
D. C es transforma en E per passar, per
construcció, la circumferència d'inversió pel punt
mig del segment CE.
- Tracem
la recta euclidiana que uneix els punts C i E.
- Considerem
el punt d'interecció de la recta anterior amb la recta de
l'infinit. Aquest punt, P,
és el centre de la circumferència d'inversió.
- Mesurem el
radi, r, de la
circumferència d'inversió. Ho podem fer seleccionant la
circumferència i seleccionant l'eina "Measure/Radius".
- Calculem a
la distància que es troba la imatge del punt D per la inversió que estem
considerant. Podem trobar aquesta distància a partir de la
definció de les inversions, és a dir, a partir de la
fórmula: PD = r·r/PC.
- Tracem la
circumferència euclidiana de centre P i radi el resultat anterior.
- Tracem la
recta euclidiana que uneix els punts P
i D.
- Considerem
la intersecció de la circumferència de (7) amb la recta
de (8). Aquest punt, F,
és la imatge de D per
la inversió.
- Tracem la bisectriu hiperbòlica
de l'angle que té per vèrtex el punt E i per semirectes la EF i el raig donat.
Considerem
la circumferència que determina la bisectriu com a
circumferència d'una altra inversió. Apliquem la
inversió als punts E
i F. El punt E és fix per la
inversió per pertànyer a la circumferència
d'inversió. Com que les inversions conserven els angles, el raig
EF es transforma amb el raig
donat. Així, la imatge del punt F per aquesta inversió ens
determinarà l'extrem final del segment transportat. Ara no podem
seguir un mètode anàleg al dels passos (3)-(9)
perquè el punt del que sabem la imatge és un punt fix,
per tant, no podem traçar la recta pel punt i la seva imatge.
- Tracem el segment que uneix els
punts E amb el punt d'intersecció de la bisectriu amb la recta
de l'infinit.
- Considerem
el punt mig euclidià del segment anterior.
- Tracem la
recta perpendicular al segment que passa pel punt mig.
- Considerem
el punt d'intersecció de la recta anterior amb la recta de
l'infinit. Aquest punt és el centre de la circumferència
d'inversió ja que ha estat construït a partir de la
mediatriu d'un segment que uneix dos dels punts de la
circumferència.
- Tracem la
recta euclidiana que uneix el punt anterior amb el punt F.
- Considerem
la intersecció, J,
d'aquesta recta amb el raig donat. Aquesta és la imatge de F i
l'extrem del segment que buscàvem.
- Tracem el segment hiperbòlic que
té per extrems els punts E
i J. Aquest segment
hiperbòlic és el transportat del segment CD.
Llista d'eines
Geometria
hiperbòlica