Triangle hiperbòlic equilàter
A la Geometria
Hiperbòlica no existeixen els triangles semblants. Això
és conseqüència de la relació entre longituds
i angles que ens proporciona la fórmula de l'angle de paral·lelisme.
La no existència de triangles hiperbòlics semblants
implica l'existència d'un únic triangle equilàter
hiperbòlic fixat l'angle. Recordem que una altra de les
diferències entre la Geometria Euclidiana i la Geometria
Hiperbòlica és el valor de la suma dels angles d'un
triangle. A la Geometria Hiperbòlica aquesta suma sempre
serà inferior a dos angles rectes. Per tant, no serà
obligatori que cada un dels angles d'un triangle equilàter
tingui 60º. De fet, no trobarem cap triangle equilàter
hiperbòlic amb els angles d'exactament 60º. Si fos
així la suma dels angles d'aquest triangle seria de dos rectes,
cosa que no és possible. Es pot veure que per a qualsevol valor
entre 0 i 60º, ambdós no inclosos, tenim un únic
triangle equilàter, llevat d'isometries.
Anem a construir un triangle equilàter hiperbòlic.
Per construir el triangle hiperbòlic equilàter podem
seguir els
següents passos:
- Tracem una
semirecta euclidiana qualsevol que tingui
l'origen, M a la recta de
l'infinit i que no sigui paral·lela a
aquesta.
- Considerem
dos punts, B i C diferents i qualssevol
d'aquesta semirecta. Aquests seran dos dels tres punts del
triangle.
- Busquem
la inversió amb centre a la recta de l'infinit que
transforma un punt en l'altre. El punt que talla la
circumferència
d'inversió a la semirecta estarà entre els dos punts. Per
trobar
la inversió determinarem aquest punt, de fet, el radi de la
circumferència a partir d'aquest punt. Utilitzem que
perquè un
punt sigui invers d'un altre cal que es compleixin dues
condicions. Han d'estar alineats amb l'origen de la inversió i
el
producte de la distància de cada punt a l'origen ha de ser el
radi
de la circumferència al quadrat. La primera afirmació ens
assegura
que l'origen de la inversió que estem buscant és el punt
d'intersecció de la semirecta amb la recta de l'infinit. Per
tant,
un punt de la circumferència ens la determinarà. A partir
d'imposar que els punts B i C són inversos tenim que el
radi
és √MB·MC. Tracem, doncs, la
circumferència de
centre M
i radi la longitud anterior.
Cal que el tercer punt, A,
del triangle equilàter estigui
sobre
aquesta circumferència, així podrem afirmar que el
segment
hiperbòlic AB es
transforma en l'AC ja que A serà
fix i B
i C són inversos.
- Tracem la circumferència
hiperbòlica de centre B
i radi BC.
- Considerem
un dels dos punts d'intersecció d'aquesta
circumferència hiperbòlica amb la circumferència
d'inversió.
Aquest punt serà el tercer vèrtex del triangle
equilàter
hiperbòlic que volíem construir.
Aquesta
construcció ens dóna un triangle equilàter ja que
tenim
que la longitud de tots els costats és la mateix. Podem provar
aquesta afirmació a partir de provar que la longitud d'un costat
és la mateixa que la dels altres dos. Per pertànyer A a
la
circumferència d'inversió que transforma B en C tenim
que la
longitud de AB és la
mateixa que la de AC.
Però la
longitud de AB també
és la mateixa que la de BC
ja que
també hem construït A
de manera que pertanyi a la circumferència
hiperbòlica de
centre B i radi BC i, per definició, tots
els punts d'una
circumferència equidisten del centre i la distància
és el radi.
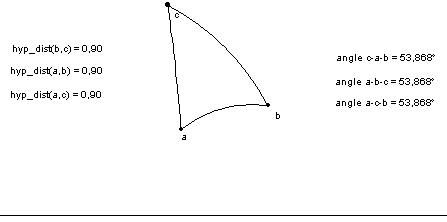
Per comprovar empíricament que realment és
equilàter podem
utilitzar la funció longitud.
Si mesurem cada un dels segments
constatarem que els tres segments tenen la mateixa longitud i, per
tant, el triangle és equilàter. També podem
mesurar els angles i veurem
que tots tres
també tenen
la mateixa amplitud (i que aquesta ve determinada per la
longitud
dels segments).
També
podem construir el triangle equilàter d'una altra manera.
Utilitzarem que els punts d'una circumferència tenen la
propietat d'estar tots a la mateixa distància del centre.
Així podem seguir els següents passos:
- Marquem dos
dels vèrtexs del triangle equilàter, A, B.
- Tracem la circumferència
hiperbòlica amb centre el primer punt i que passi pel segon.
- Tracem la circumferència
hiperbòlica amb centre el segon punt i que passi pel primer.
- Considerem
els punts d'intersecció de les dues circumferències.
Aquests dos punts estan a la mateixa distància de cada un dels
dos punts fixats. Això és perquè pertanyen a les
dues circumferències amb centre cada un dels punts.
- Tracem el triangle hiperbòlic que
té per
vèrtexs els dos punts fixats i un dels dos punts
d'intersecció del pas anterior. Aquest triangle és
equilàter.
Per provar que el
triangle és equilàter només cal veure que la
longitud de cada un dels costat és la mateixa. La longitud del
costat AC és igual
que la del costat AB per ser
B i C dos punts de la
circumferència hiperbòlica amb centre A. La longitud del costat AB també és igual
que la del costat BC per ser
A i C dos punts de la
cirucmferència amb centre B. Per
tant, la longitud dels tres costats és la mateixa. Així
el triangle és quilàter.
Movent els vèrtexs fixats obtindrem tots els altres triangles
equilàters. Igual que abans podem
comprovar empíricament que el triangle obtingut realment
és equilàter.
Triangles
Geometria
hiperbòlica