L’objectiu de la regla de D’Hondt és repartir escons entre partits proporcionalment als vots que han rebut.
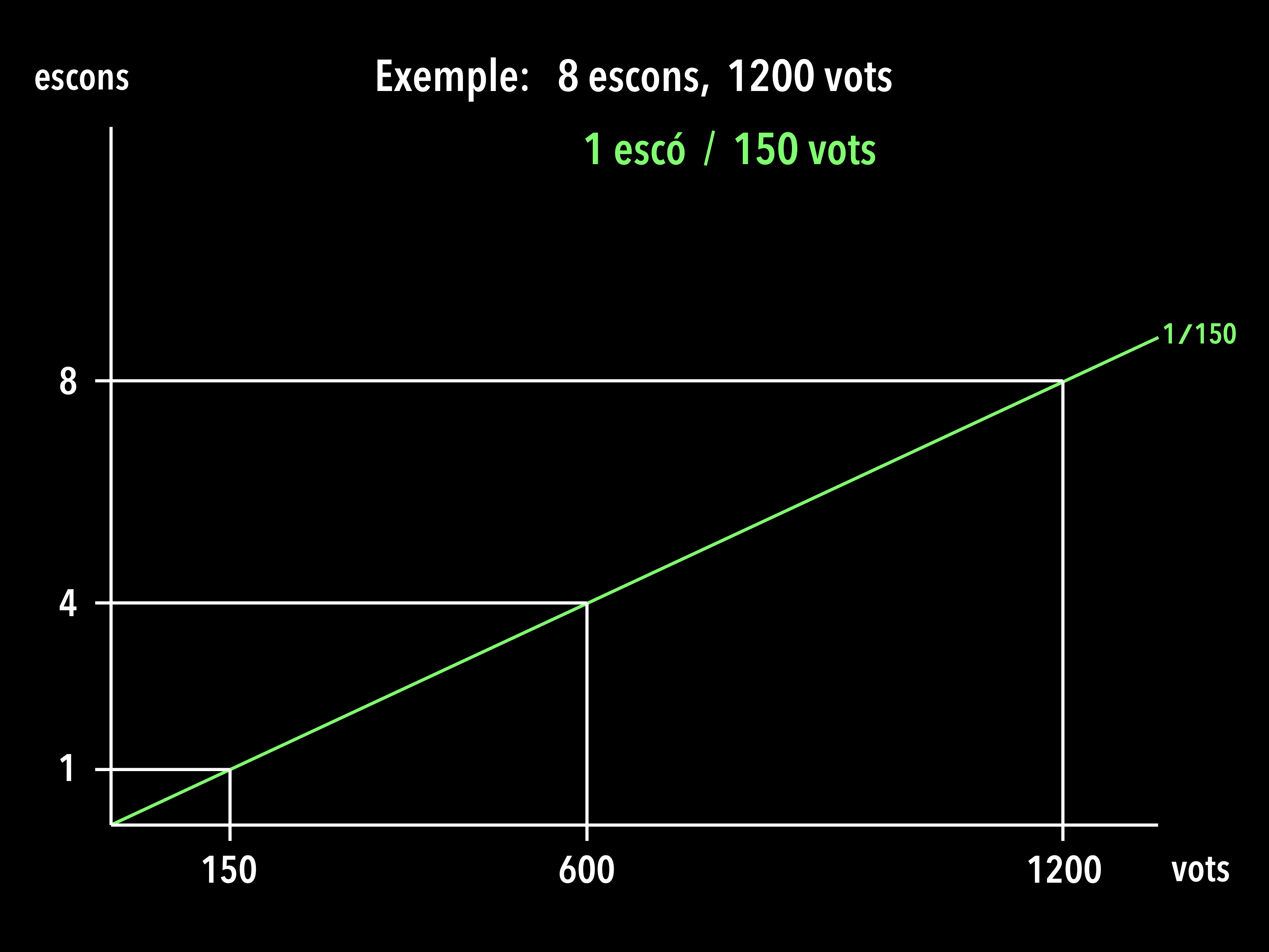
A vegades hi ha una sola manera de repartir proporcionalment els vots, no cal la regla de D’Hondt. Per exemple, si tenim 8 escons a repartir i s’han emès 1200 vots, la regla de proporcionalitat ens diu que 150 vots tindran 1 escó, 600 vots donaran 4 escons. Diem que cada escó “costa” 150 vots. Representem-ho gràficament. La recta en verd ens dóna el nombre d’escons que correspon a cada nombre de vots (la recta té pendent 1/150).
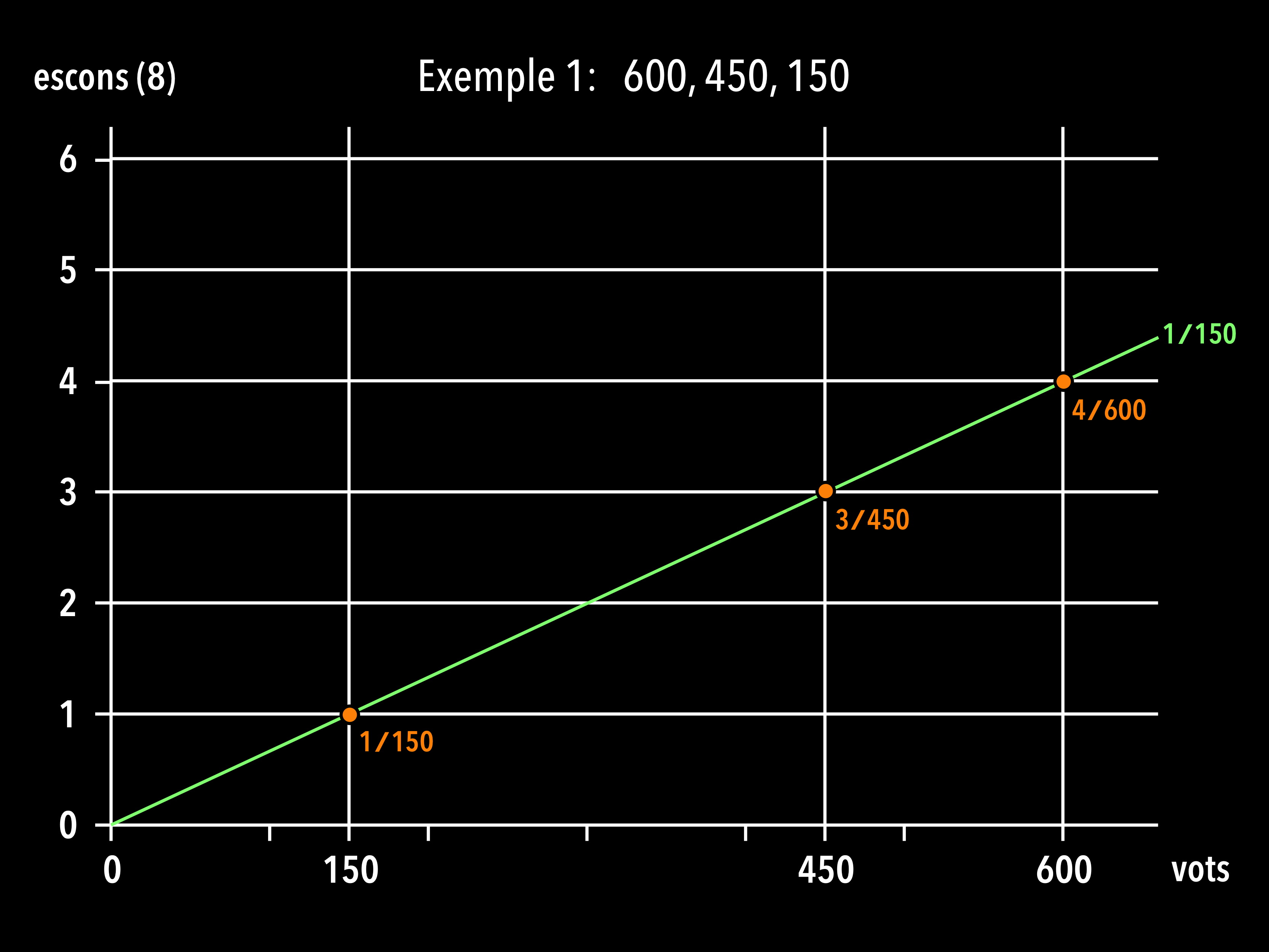
Exemple 1: Suposem que en unes eleccions amb 1200 vots el partit A rep 600 vots, el B en rep 450 i el C 150. El repartiment d’escons és clar per la regla de proporcionalitat:
Exemple 2: Però, com ho faríem si no fos tan exacte? Modifiquem l’anterior exemple lleugerament. Suposem ara que els 1200 vots es repartissin A: 610, B: 430 i C: 160.
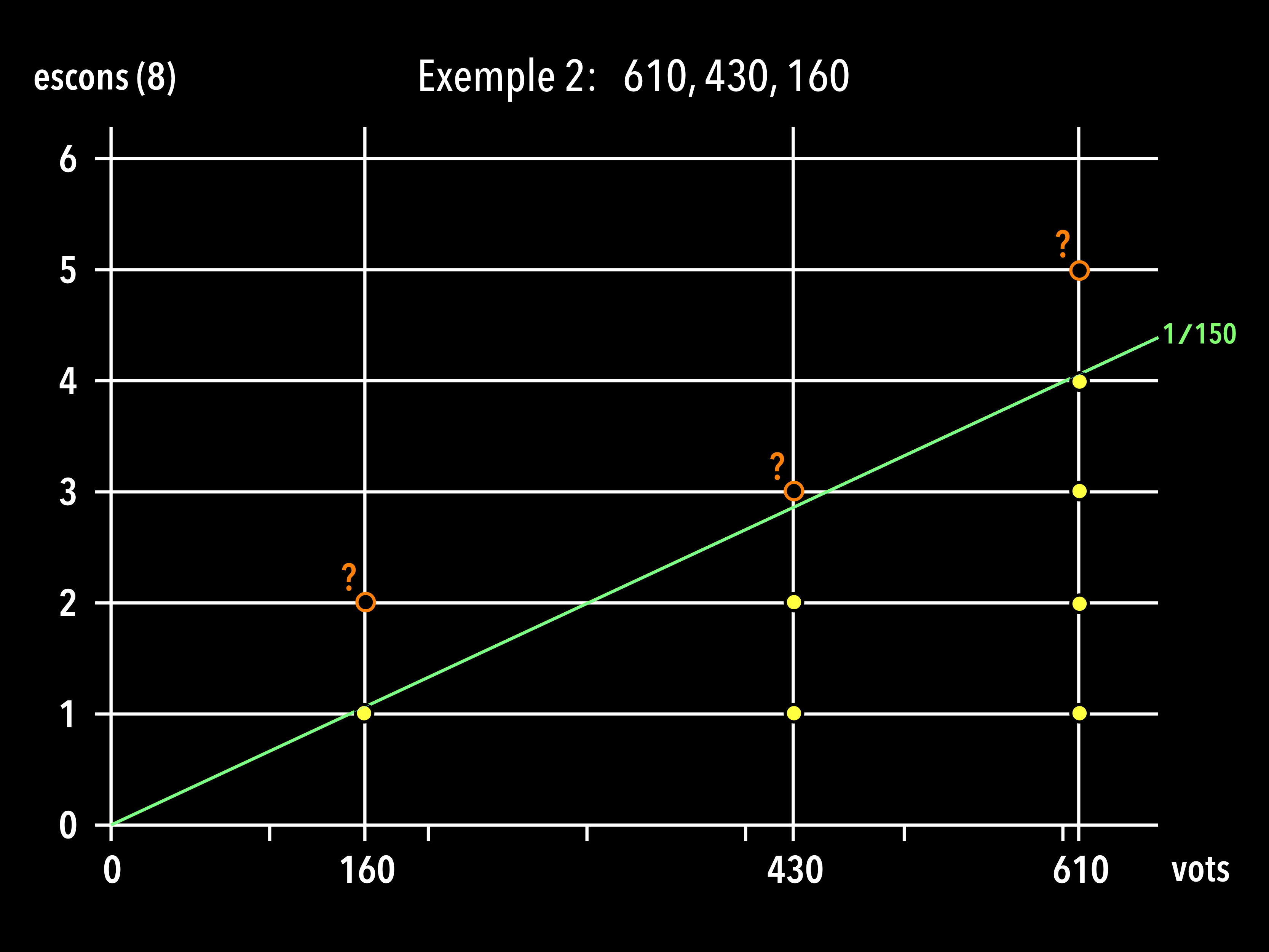
Al partit A li corresponen almenys 4 escons, al B, almenys 2 i al C, almenys 1. Però amb aquest criteri ens queda un escó per repartir. La qüestió és, a quin partit li assignem el vuitè escó? Aquí entra la regla de D’Hondt (o, alternativament, qualsevol altra regla de repartiment d’escons, com ara Sainte-Laguë o Restes Majors).
Sigui quina sigui l’assignació del vuitè escó, el preu pagat per escó variarà d’un partit a un altre, ja no serà exactament 150 (el preu que dóna la proporcionalitat exacta).
La regla de D’Hondt procura que el preu mínim per escó, entre els preus pagats pels partits, sigui el més gran possible.
Calculem quin seria aquest preu mínim per a les diferents possibles assignacions del vuitè escó:
- si l’assignem al partit A, aleshores el preu per escó mínim el té A, val 610/5 = 122;
- si l’assignem al partit B, aleshores el preu per escó mínim el té B, val 430/3 = 143.3;
- si l’assignem al partit C, aleshores el preu per escó mínim el té C, val 160/2 = 80.
Per tant, la regla de D’Hondt assigna el vuitè escó al partit B.
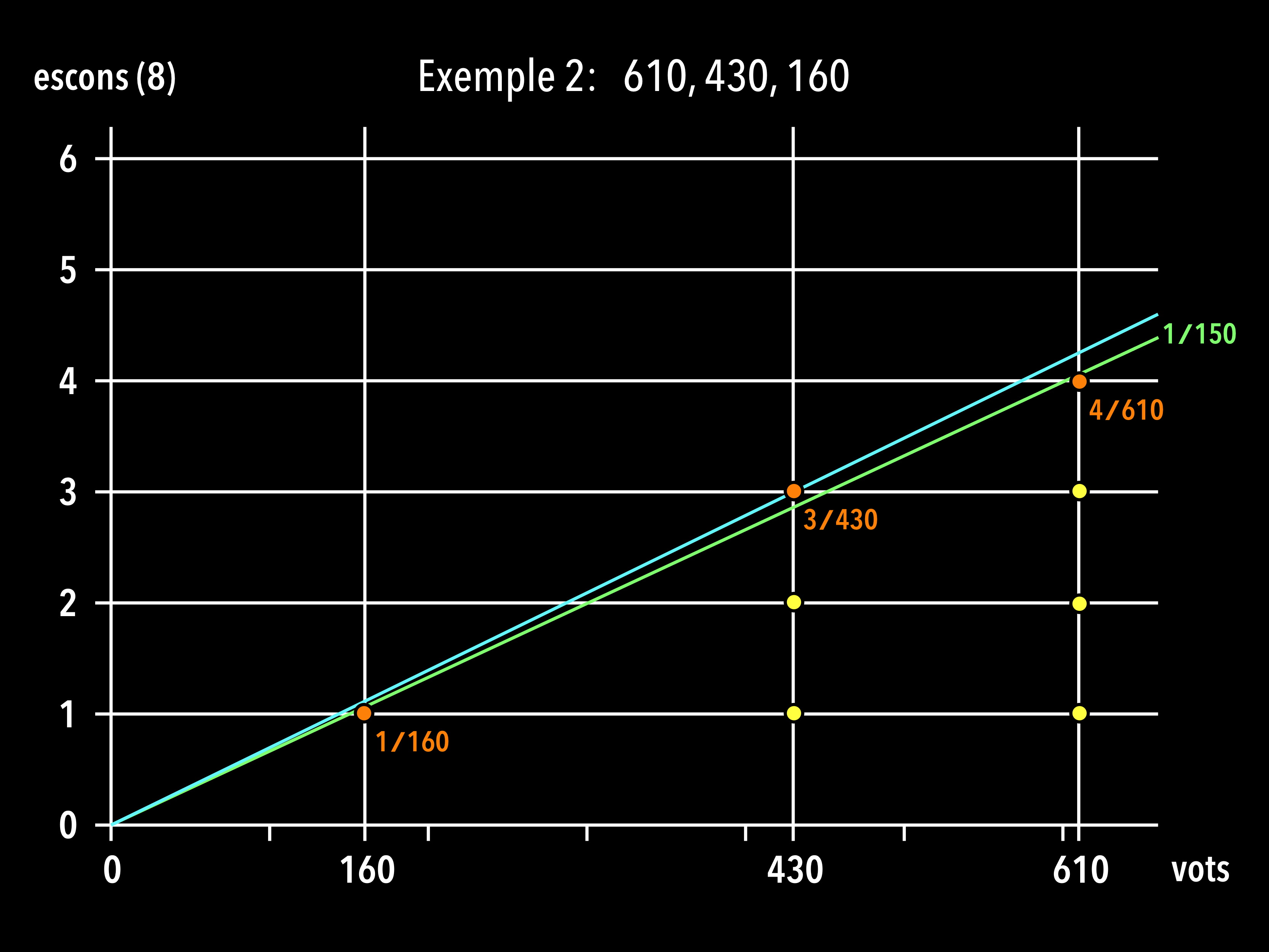
Podem representar gràficament el que hem fet, que no és més que anar baixant el preu per escó, des de 150, augmentant el pendent de la recta verda de proporcionalitat, fins que aquesta arribi a passar per un dels interrogants (possibles assignacions del vuitè escó).
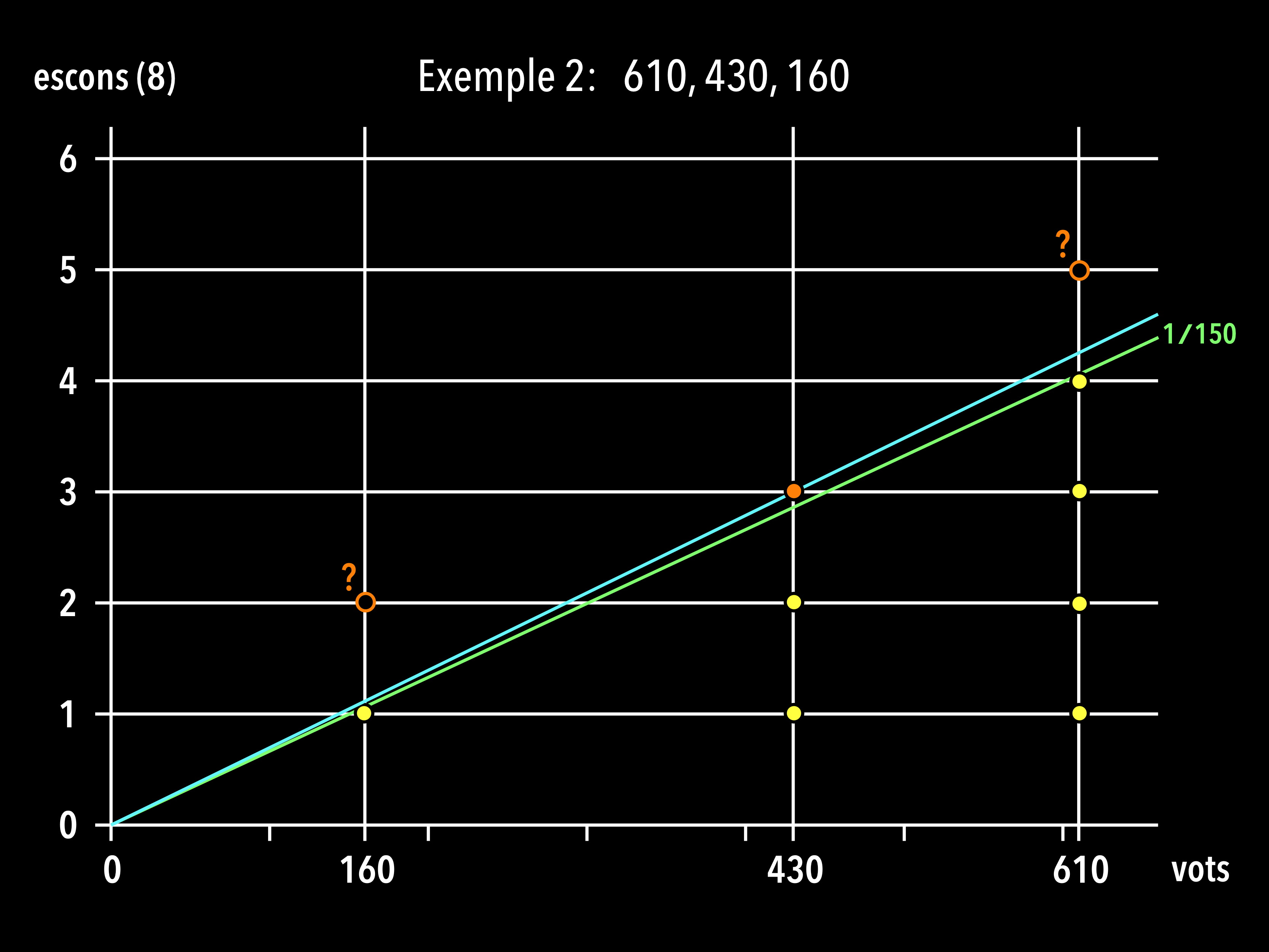
La recta en verd té pendent 1/150 i la recta en blau, que passa pel punt en taronja del partit B, té pendent 3/430 = 1/143.3. Que aquest sigui el primer punt al que arribem quan augmenta el pendent de la recta verda (la de proporcionalitat exacta) significa que el partit B paga un preu per escó menor que 150 (el preu “ideal”) però que aquest preu és el més proper possible a 150. Aquest és el repartiment per al qual el preu mínim per escó, entre els preus pagats pels partits, és el més gran possible.
D’aquesta manera, el preu que paguen els tres partits, en vots per escó, és: A: 610/4 = 152.5, B: 430/3 = 143.3, C: 160/1 = 160.
Exemple 3: Fem el repartiment en un altre cas. Suposem que els 1200 vots es distribueixen de la manera següent: A: 640, B: 360, C: 200. Començant en el preu ideal, 150 vots per escó, calculem quants escons correspondrien a cada partit: A: 640/150 = 4.3, B: 360/150 = 2.4, C: 200/150 = 1.3.
Torna a sobrar un escó. Per repartir-lo, com abans, ho fem gràficament. Partim de la recta de proporcionalitat exacta i augmentem el seu pendent.
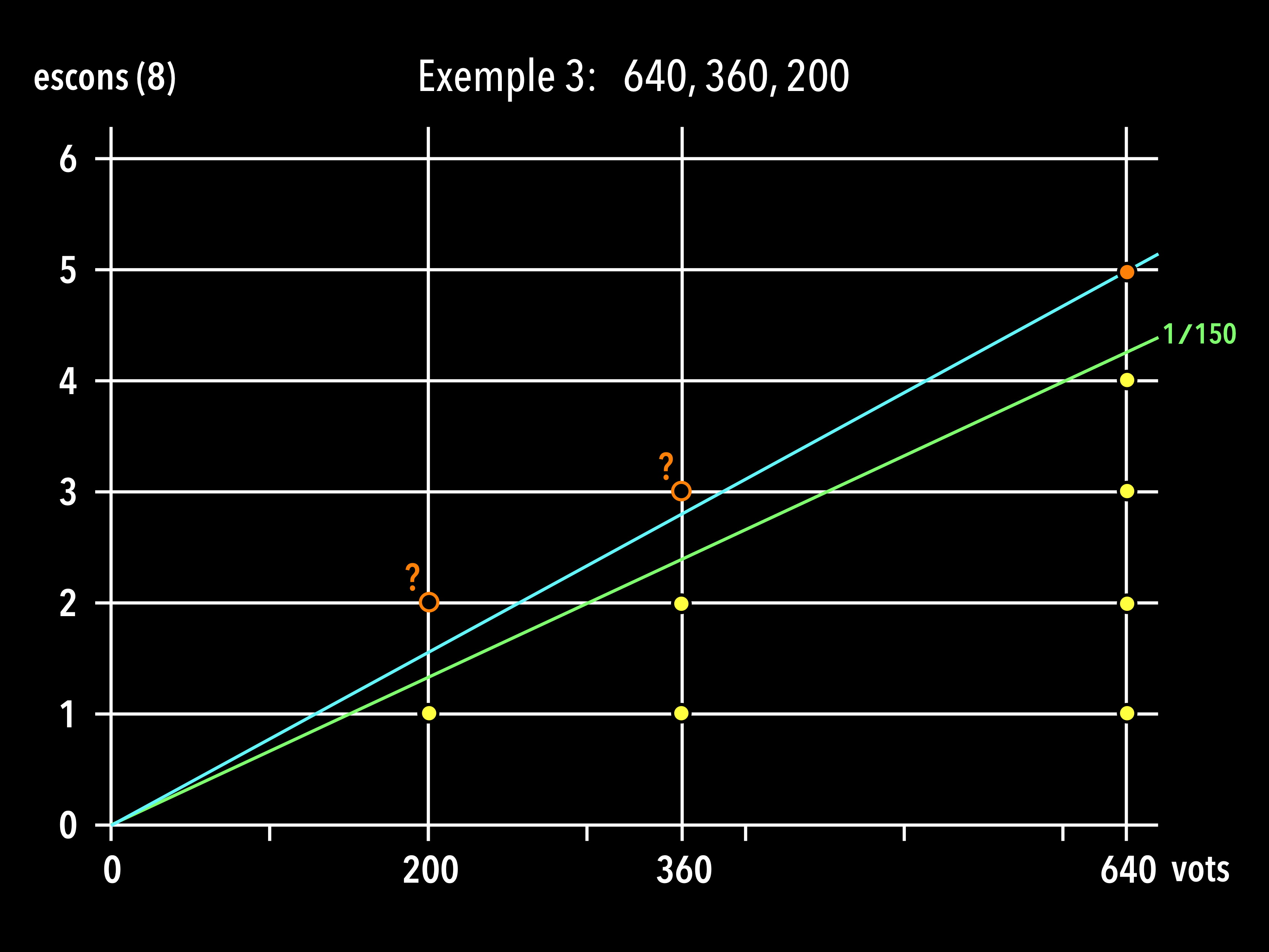
La línia blava ens dóna l’assignació del vuitè escó a la candidatura A, que té 640 vots. Ara els preus en vots per escó que paguen els tres partits són: A: 640/5 = 128, B: 360/2=180, C: 200/1=200.
El partit A paga menys vots per escó que els altres, però el preu encara seria menor —i per tant més desigual en el sentit de D’Hondt— si haguéssim assignat el vuitè escó a B (pagaria només 120 vots) o a C (en pagaria només 100).
Quina és la relació amb l’algorisme habitual? L’algorisme d’assignació d’escons per la regla de D’Hondt que s’utilitza habitualment no és aquest que hem explicat. El que es fa és posar els partits per columnes i, en files, dividir els seus vots per 1, per 2, per 3, etc. La taula corresponent a l’exemple 3 és:
| A | B | C |
|---|---|---|
| 640 / 1 = 640 | 360 / 1 = 360 | 200 / 1 = 200 |
| 640 / 2 = 320 | 360 / 2 = 180 | 200 / 2 = 100 |
| 640 / 3 = 213.3 | 360 / 3 = 120 | 200 / 3 = 66.7 |
| 640 / 4 = 160 | 360 / 4 = 90 | 200 / 4 = 50 |
| 640 / 5 = 128 | 360 / 5 = 72 | 200 / 5 = 40 |
| … | … | … |
Un cop feta la taula, l’algorisme va assignant els 8 escons de manera successiva als partits que tenen números més alts a la taula:
El número més gran és 640, per tant el primer escó va a A, el següent és 360, a la columna de B, per tant el segon escó va a B. El tercer escó és per a A, el quart també per a A, el cinquè per a C, el sisè per a B, el setè per a A i, finalment, el vuitè per a A.
A la taula s’hi pot llegir el preu per escó que ha pagat cada partit. El preu es fixa quan se li assigna el darrer escó dels que rep: A paga 128 vots per escó, B en paga 180 i C en paga 200.
Aquest algorisme s’assembla molt al que hem donat més amunt. Podem mirar-ho com si comencéssim amb una recta de pendent zero i anéssim augmentant el seu pendent fins arribar a cobrir els 8 escons que volem assignar. En anar pujant, el primer partit que rep un escó és A, el segon és B, etc (en el mateix ordre que l’algorisme habitual):
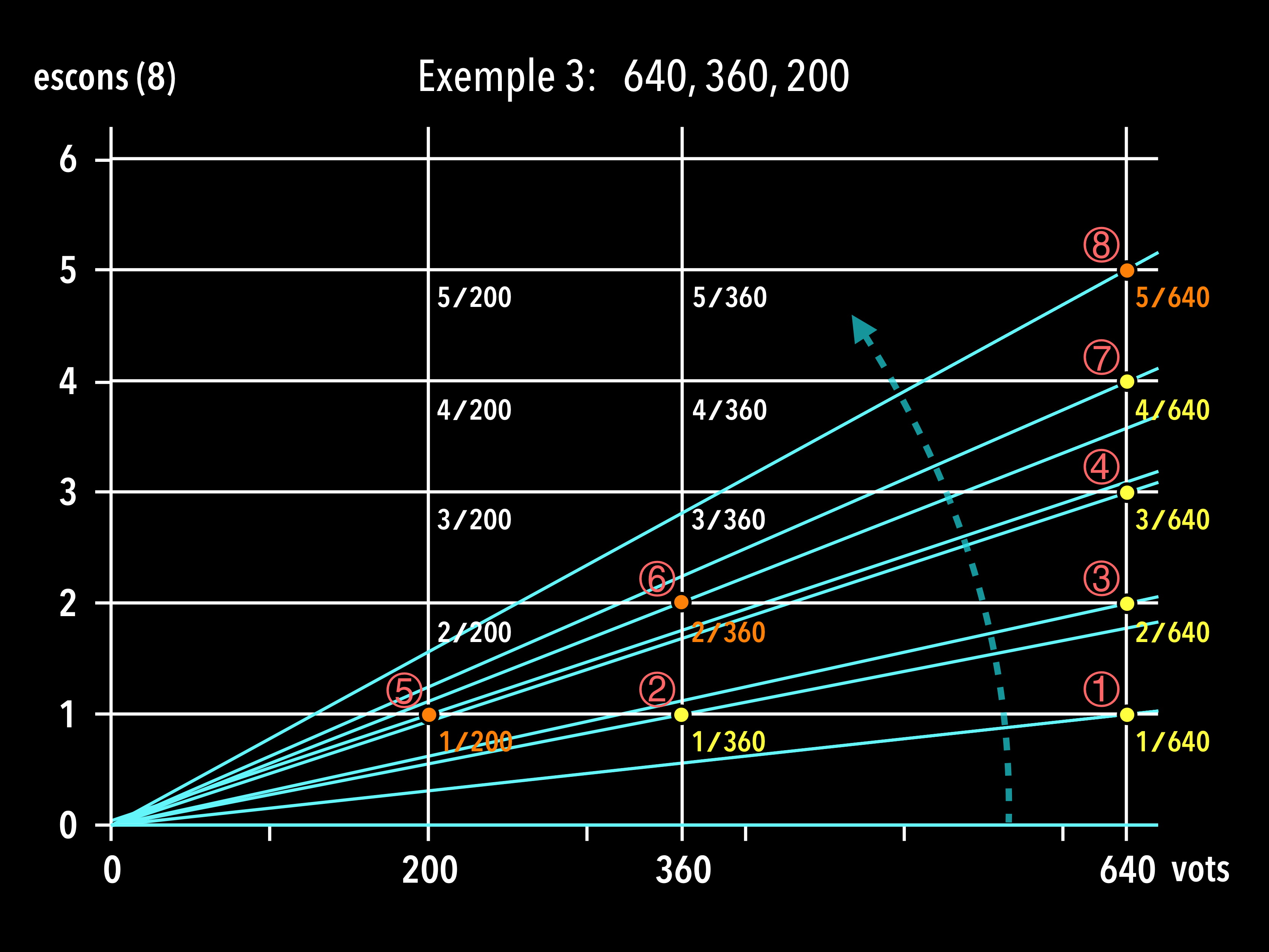
Hem vist, doncs, que el mètode de D’Hondt busca acostar-se a la proporcionalitat exacta seguint un criteri molt concret: que els votants més afavorits ho siguin el mínim possible. ❀
(Gràfics basats en una idea d’Eduard Hagenbach-Bischoff, 1885)