Amb motiu de les dificultats que presenta l’elecció del President de la Generalitat de Catalunya per a la propera legislatura, aquests dies té lloc a través de Twitter un interessant experiment on es planteja un procediment d’elecció mitjançant un sistema d’eliminatòries, ben bé com si es tractés d’una competició esportiva (@JordiCalvís #RoadToTheConsensus). Es va començar amb 128 candidats (135 menys els 7 de la mesa) amb els quals es van plantejar a l’atzar 64 enfrontaments per parelles. Cada parella és objecte de votació, dins d’un termini especificat, la qual cosa determina quin dels dos candidats passa a la següent eliminatòria. La figura següent mostra els enfrontaments de setzens de final.

La validesa d’aquest experiment està limitada pel fet que els votants formen un conjunt petit i molt particular. Suposem, però, que hi participés tota la població. Seria un bon procediment?
El seu principal inconvenient és el mateix que presenta aquest sistema en les competicions esportives: el resultat final pot dependre de quins siguin els aparellaments inicials. Per exemple, amb quatre candidats A, B, C, D pot passar perfectament que si enfrontem A amb B i d’altra banda C amb D acabi guanyant A, mentre que si enfrontem A amb C i d’altra banda B amb D acabi guanyant un candidat diferent de A. Aquest fenomen pot passar encara que en totes les votacions hi participin els mateixos votants i aquests mantinguin invariables les seves preferències sobre els candidats.
No costa gaire de comprovar que la situació que hem dit es produeix si les preferències dels votants són, per exemple, les següents:
- 2,5 milions de votants prefereixen un candidat a l’altre segons l’ordre A > B > C > D,
- 2 milions els ordenen B > C > D > A,
- 1,5 milions els ordenen C > D > A > B.
En efecte, amb aquestes preferències, els enfrontaments A contra B i C contra D donen com a resultat que A guanya B per 4 a 2 (milions de votants), C guanya D per unanimitat, i en la final C guanya A per 3,5 a 2,5. En canvi, amb les mateixes preferències, els enfrontaments A contra C i B contra D donen que C guanya A, per 3,5 a 2,5, B guanya D, per 4,5 a 1,5, i en la final B guanya C per 4,5 a 1,5.
Això de que el resultat final pugui dependre de quins siguin els aparellaments inicials és certament indesitjable.
Aquesta mena de problemes són típics de quan es tracta d’elegir entre més de dos candidats en base a les preferències que els votants puguin expressar sobre ells. Tal com diem a l’entrada Votacions amb més de dues opcions, en Ramon Llull ja es va ocupar d’aquestes qüestions fa més de 700 anys! De fet, un dels dos procediments que va considerar és essencialment un sistema d’eliminatòries. L’altre procediment considerat per Llull té l’avantatge que el resultat no depèn de cap element aliè a les preferències dels votants. I també té un anàleg en el món de l’esport: en lloc d’un sistema d’eliminatòries ara es tracta essencialment de considerar tota una lliga i comptar quants enfrontaments guanya cada candidat.
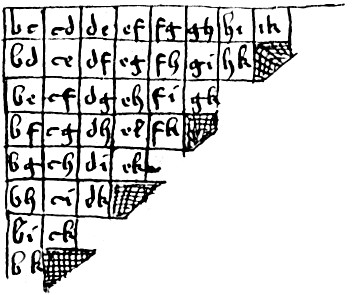
Taula on Ramon Llull considerava totes les parelles de candidats (còpia del segle XV)
Això sí, en principi aquest procediment demana les preferències dels votants sobre qualsevol parella de candidats, la qual cosa és impensable amb 128 candidats. Tanmateix, actualment hi ha altres procediments que tenen el mateix esperit però permeten tractar el cas en què cada votant expressa les seves preferències mitjançant un rànquing truncat, és a dir una ordenació dels seus candidats més preferits.
Per a més detalls referim el lector a l’article Votar, no tan fàcil com sembla, però podríem fer-ho millor! (que no entra, però, en el cas de preferències incompletes). ❀