Quan es parla de paritat de gènere en unes eleccions, tothom té clar que basta tenir una llista ordenada de candidates dones i una altra de candidats homes i fer una “cremallera”, és a dir anar prenent alternativament noms d’una i altra llista.
Un cas similar seria el d’unes eleccions on només s’haguessin presentat dos partits i haguéssin obtingut el mateix nombre de vots. En aquest cas també és obvi que correspon combinar les dues llistes mitjançant una cremallera.
I si els dos partits, diguem-ne A i B, haguessin obtingut un d’ells el doble de vots que l’altre? Llavors és prou clar que el que correspon és prendre alternativament dos candidats de A i un de B, fins arribar al nombre d’escons que estiguem repartint. En particular, no correspon elegir els candidats més votats, que serien tots ells del partit A.
I si els nombres de vots obtinguts per A i B són més generals? Suposem, per exemple, que fossin 2800 i 1200. Com que aquests dos nombres estan en la relació de 7 a 3, ja es veu que hi hauria d’haver 7 candidats de A per cada 3 de B. Però en general el nombre d’escons a repartir no serà un múltiple de 10. Per tant, cal especificar la seqüència concreta d’aquesta cremallera més complicada. Una possibilitat seria, per exemple, AABAABAABA (repetida ad infinitum). Una altra seria ABAABAAABA, que es pot veure com un desplaçament de la precedent. I també podem considerar, per exemple, la seqüència AAABAAABAB, o fins i tot AAAAAAABBB… Quina d’aquestes múltiples possibilitats adoptem? L’última que hem posat té l’inconvenient que inicialment el repartiment dels escons s’aparta molt de la proporció 7:3. Des d’aquest punt de vista, les millors seqüències són les dues primneres. Noti’s també que només hem considerat seqüències que comencin per A, ja que altrament en el cas d’un sol escó l’estaríem donant al partit menys votat.
La regla de D’Hondt és un procediment general que determina aquesta seqüència de cremallera a partir dels nombres de vots. I la regla de Sainte-Laguë n’és un altre. En el cas concret dels nombres de vots considerats al paràgraf precedent, aquestes regles resulten respectivament en les dues seqüències que hem dit en primer i segon lloc. Més concretament, resulten en les seqüències AABAABAA(BA) i ABAA(BA)AABA, on els parèntesis indiquen una indeterminació entre la seqüència BA i la seqüència AB (la qual indeterminació es produeix a causa de que 2800/7 = 1200/3).
En el cas de la regla de D’Hondt, el criteri que determina la cremallera és que els electors més “afavorits” ho siguin el menys possible. Aquí entenem que un elector és més o menys afavorit en la mesura que obtingui més o menys representació; la quantitat de representació que obté un elector és el nombre d’escons que ha rebut el seu partit dividit pel nombre d’electors que l’han votat.
Així, en l’exemple anterior el primer escó és assignat al partit A, perquè d’aquesta manera els electors més afavorits obtenen una representació de 1/2800, que és certament inferior a 1/1200, el valor que s’obtindria en assignar aquest primer escó al partit B. El segon escó també el rep el partit A, perquè 2/2800 = 1/1400 encara és inferior a 1/1200. En canvi, el tercer escó va a parar a B, perquè 1/1200 és inferior a 3/2800. I així successivament.
Si en lloc d’aquests quocients, com més petits millor, considerem els seus inversos, com més grans millor, arribem així a la coneguda recepta de dividir els nombres de vots per 1,2,3,4,5, etcètera i prendre els quocients més grans fins al nombre d’escons que estiguem repartint.
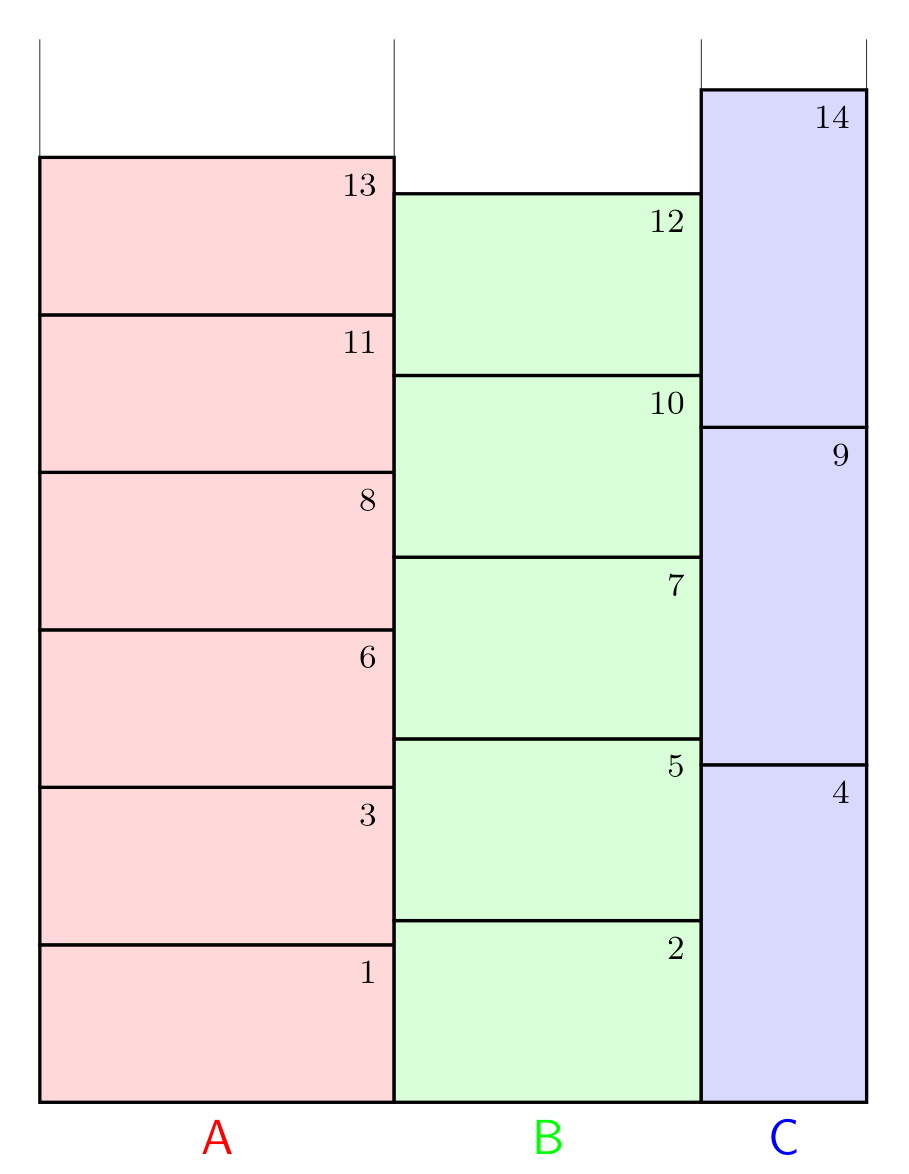
D’altra banda, aquest procediment s’estén sense problema a un nombre arbitari de partits. La figura 1 il·lustra gràficament el cas de tres partits A, B i C que han obtingut respectivament 1500, 1300 i 700 vots. Sobre l’eix horitzontal hem marcat tres segments de longituds proporcionals a aquests nombres de vots. Sobre cadascun d’aquests segments hi ha una pila de rectangles que representen escons. Tots ells tenen la mateixa àrea; no solament els d’una mateixa columna, sinó també els de columnes diferents. Com que les bases no són iguals, les altures tampoc no ho són: per a aconseguir que les àrees siguin iguals, les altures han de ser proporcionals respectivament a 1/1500, 1/1300 i 1/700. Aquests nombres representen la fracció d’escó que toca a cada votant de A, B i C quan un escó d’aquell partit es divideix a parts iguals entre els seus votants. Els números que posem a la part dreta superior de cada rectangle especifiquen la seqüència d’assignació d’escons. D’acord amb el que hem dit més amunt, aquesta seqüència és simplement la que resulta d’anar prenent sempre el següent nivell més baix.
La idea precedent es pot estendre fins i tot al cas de llistes obertes, sense partits. Aquesta extensió es deu al matemàtic suec Edvard Phragmén. La figura 2 il·lustra la seva aplicació a un cas amb 10 candidats a, b, c, d, e, f, g, h, i, j i 1000 electors, els quals voten com segueix:
- 100 electors aproven només el candidat a.
- 350 electors aproven els candidats a, b, c, d, e.
- 100 electors aproven els candidats c, d, e, f, i, j.
- 150 electors aproven els candidats e, f, g.
- 300 electors aproven els candidats f, g, h, i, j.
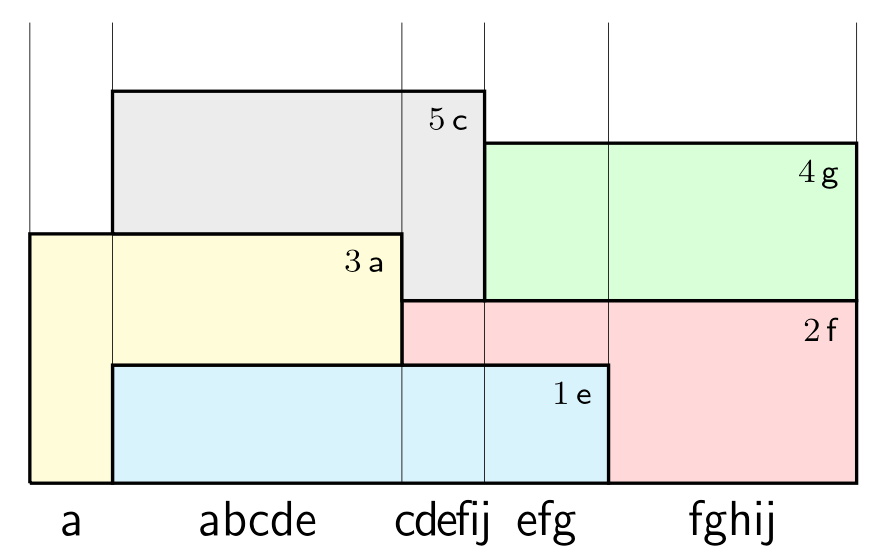
A diferència del cas de D’Hondt, aquí els escons estan representats per unes figures no necessàriament rectangulars. La raó d’això és que ara un escó no es reparteix necessàriament a parts iguals entre els electors que han votat aquell candidat: Si la representació que ja tenen aquests electors no és uniforme, llavors el nou escó no es reparteix de manera uniforme, sinó que alguns d’aquests electors en reben un fracció més gran que els altres, de tal manera que després d’aquest repartiment tots ells tinguin exactament el mateix nivell de representació. En cada pas s’escull el candidat que fa que aquest nou nivell sigui el més baix possible. Així doncs, la idea és ben bé la mateixa que més amunt amb el procediment de D’Hondt. Només que ara els càlculs són més entretinguts. Per més detalls, referim a la pàgina El mètode de Phragmén.
Però la idea de fons és sempre la mateixa: que la distribució de representació entre els electors sigui el més equitativa possible. ❀